Vierstreckensatz: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K |
|||
| Zeile 46: | Zeile 46: | ||
:Das Längenverhältnis von Strecken ist wegen der Eigenschaft der '''Längenverhältnistreue''' | :Das Längenverhältnis von Strecken ist wegen der Eigenschaft der '''Längenverhältnistreue''' | ||
:gleich, so auch <math>{\overline{ZA}\over\overline{ZA'}}</math> = <math>{\overline{ZB}\over\overline{ZB'}}</math>. | :gleich, so auch <math>{\overline{ZA}\over\overline{ZA'}}</math> = <math>{\overline{ZB}\over\overline{ZB'}}</math>. | ||
| − | :Dies bedeutet, dass sich | + | :Dies bedeutet, dass sich die Abschnitte auf der einen Halbgeraden genauso verhalten, wie die Abschnitte auf der anderen |
| − | :Halbgeraden | + | :Halbgeraden. Diesen Satz nennt man den '''ersten Vierstreckensatz'''. |
:Einsetzen der Werte ergibt: <math>{\overline{1 Zoll}\over\overline{2,54 cm}}</math> = <math>{\overline{15 Zoll}\over\overline{x cm}}</math> | :Einsetzen der Werte ergibt: <math>{\overline{1 Zoll}\over\overline{2,54 cm}}</math> = <math>{\overline{15 Zoll}\over\overline{x cm}}</math> | ||
:x berechnet sich zu 38,1 cm. | :x berechnet sich zu 38,1 cm. | ||
Version vom 5. Juli 2009, 17:55 Uhr
|
Lernpfad
|
1. Station: Erster Vierstreckensatz
- Zoll ist eine Längeneinheit die im Alltag häufig zu finden ist, z.B. bei Laptops, Computern und Fernsehern.
- Um sich die Größe besser vorstellen zu können, soll die Einheit Zoll in Zentimeter umgerechnet werden.
- Hierfür gibt es zwei Möglichkeiten:
- die algebraische Berechnung
- oder die geometrische.
- Als Bepsiel nehmen wir die Umrechnung von einem 15 Zoll Laptop.
- Finde heraus wie du die Aufgabe algebraisch lösen kannst:
- Gegeben: Der Laptop hat einen 15 Zoll Bildschirm. 1 Zoll entspricht 2,54 cm.
- Gesucht: Umrechnung von 15 Zoll in cm.
- Lösung: Berechne in deinem Heft und trage hier deine berechnete Lösung mit Angabe der Einheit (cm) ein!
15 Zoll entsprechen 38,1 cm (Tipp: Berechne mit Hilfe des Dreisatzes).
- Im Folgenden wird dir gezeigt, wie du die Aufgabe geometrisch lösen kannst.
Klicke die Schritte nacheinander an:
1. Schritt: Zeichne zwei Halbgeraden mit gemeinsamen Anfangspunkt Z und trage auf diesen Halbgeraden
- die Längen 1 cm und 15 cm ab. Benenne die Endpunkte der Strecken mit A und B.
2. Schritt: Verbinde Punkt A mit Punkt B.
3. Schritt: Trage in Z die Strecke [ZA'] mit ZA' = 2,54 cm ab.
4. Schritt: Zeichne eine Parallele durch A' zu [AB].
5. Schritt: Benenne Schnittpunkt mit B'.
6. Schritt: Miss ZB' ab.
- Rechnung die dahinter steckt:
- Vorrausgesetzt wird dass die Gerade A'B' zu AB parallel ist. Das Dreieck A'ZB' kann somit als das Bild des Dreiecks AZB
- mit dem Streckungszentrum Z aufgefasst werden. Der Punkt A wurde also auf den Punkt A' und Punkt B wurde auf Punkt B' abgebildet.
- Das Längenverhältnis von Strecken ist wegen der Eigenschaft der Längenverhältnistreue
- gleich, so auch
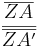 =
= 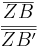 .
.
- Dies bedeutet, dass sich die Abschnitte auf der einen Halbgeraden genauso verhalten, wie die Abschnitte auf der anderen
- Halbgeraden. Diesen Satz nennt man den ersten Vierstreckensatz.
- Einsetzen der Werte ergibt:
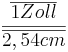 =
= 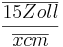
- x berechnet sich zu 38,1 cm.



