Lineare Funktionen (Stefan Gaubitz): Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Die Seite wurde neu angelegt: Gegeben ist die Funktion <big>'''''f(x) = m·x + t'''''</big> mit <math>m,t \in \mathbb{R} </math>. <u>Aufgabe 1</u> Zunächst ist <math>t=0</math> und die Funktion l...) |
|||
| Zeile 1: | Zeile 1: | ||
Gegeben ist die Funktion <big>'''''f(x) = m·x + t'''''</big> mit <math>m,t \in \mathbb{R} </math>. | Gegeben ist die Funktion <big>'''''f(x) = m·x + t'''''</big> mit <math>m,t \in \mathbb{R} </math>. | ||
| − | + | ==Aufgabe 1== | |
Zunächst ist <math>t=0</math> und die Funktion lautet <big>'''''f(x) = m·x'''''</big>. | Zunächst ist <math>t=0</math> und die Funktion lautet <big>'''''f(x) = m·x'''''</big>. | ||
| Zeile 17: | Zeile 17: | ||
| − | + | ==Aufgabe 2== | |
Nun ist <math>m=1</math> und die Funktion lautet <math>f(x)=x+t</math>. | Nun ist <math>m=1</math> und die Funktion lautet <math>f(x)=x+t</math>. | ||
| Zeile 28: | Zeile 28: | ||
| − | + | ==Aufgabe 3== | |
Abschließend sind sowohl m und t variabel. | Abschließend sind sowohl m und t variabel. | ||
Verändere beide Parameter beliebig. | Verändere beide Parameter beliebig. | ||
Bestätigen sich deine Vermutungen aus Aufgabe 1 und 2? | Bestätigen sich deine Vermutungen aus Aufgabe 1 und 2? | ||
Version vom 12. Juli 2010, 19:53 Uhr
Gegeben ist die Funktion f(x) = m·x + t mit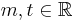 
.
Aufgabe 1
Zunächst ist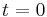 
und die Funktion lautet f(x) = m·x.
Verändere den Paramter m beliebig.
Welche Beobachtung machst du?
Was passiert bei einem negativen m?
Für was steht m in der Funktionsgleichung?
Aufgabe 2
Nun ist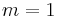 
und die Funktion lautet 
.
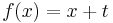Verändere den Parameter t beliebig.
Welche Beobachtung machst du? Welchen Schnittpunkt des Graphen kann man mithilfe von t direkt in der Funktion selbst ablesen?
Aufgabe 3
Abschließend sind sowohl m und t variabel. Verändere beide Parameter beliebig. Bestätigen sich deine Vermutungen aus Aufgabe 1 und 2?
