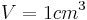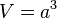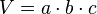Volumen: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Volumen von Würfel und Quader)
(→‎Volumen von Würfel und Quader)
Zeile 100: Zeile 100:
 
<br>
 
<br>
 
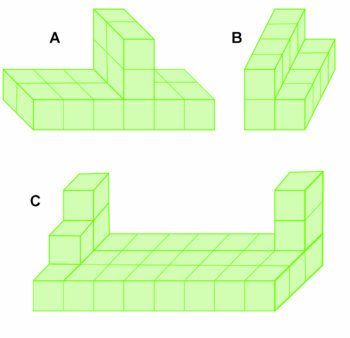
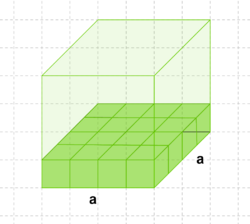
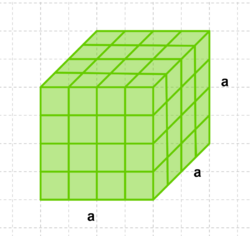
'''Die Einheitswürfel helfen uns nicht nur beim Würfel, sondern auch bei Quader. Hier müssen wir aber beachten, dass wir drei verschiedene Kantenlängen haben. Schaue dir dazu doch mal das Applet rechts an. Ziehst du an dem Punkt nach rechts, so füllt sich der Quader mit Einheitswürfeln.'''
 
'''Die Einheitswürfel helfen uns nicht nur beim Würfel, sondern auch bei Quader. Hier müssen wir aber beachten, dass wir drei verschiedene Kantenlängen haben. Schaue dir dazu doch mal das Applet rechts an. Ziehst du an dem Punkt nach rechts, so füllt sich der Quader mit Einheitswürfeln.'''
−
<div class="lueckentext-quiz">
 
−
Kannst du sagen, wie man das Volumen vom Quader berechnet? Schaue dir dazu nochmal die Schritte an, wie wir auf die Volumenformel beim Würfel gekommen sind.<br> <small>Beachte:Gib das Rechenzeichen als Wort an, z.B. für "+" schreibst du "plus", für "·" schreibst du "mal".</small> <br>
 
 
<br>
 
<br>
 +
'''Kannst du sagen, wie man das Volumen vom Quader berechnet? Schaue dir dazu nochmal die Schritte an, wie wir auf die Volumenformel beim Würfel gekommen sind.<br> <small>Beachte:Gib das Rechenzeichen als Wort an, z.B. für "+" schreibst du "plus", für "·" schreibst du "mal".</small>''' <br>
 +
<br>
 +
<div class="lueckentext-quiz">
 
Die Volumenformel für ein Quader lautet: V='''a mal b mal c(Volumen vom Quader)'''
 
Die Volumenformel für ein Quader lautet: V='''a mal b mal c(Volumen vom Quader)'''
 
</div>
 
</div>
Zeile 129: Zeile 130:
 
<div style="padding:10px;background:#ffffff;border:1px ;">
 
<div style="padding:10px;background:#ffffff;border:1px ;">
 
'''Ein großer Verpackungenhersteller muss die richtige Verpackung für ein neues Produkt finden und untersucht dafür bereits existierende Verpackungen. Die Verpackung muss groß genug sein, dass eine Füllung von 1 l reinpasst. Untersucht werden die folgenden Verpackungen (siehe auch rechts im Bild):
 
'''Ein großer Verpackungenhersteller muss die richtige Verpackung für ein neues Produkt finden und untersucht dafür bereits existierende Verpackungen. Die Verpackung muss groß genug sein, dass eine Füllung von 1 l reinpasst. Untersucht werden die folgenden Verpackungen (siehe auch rechts im Bild):
 +
<br>
 
<br>
 
<br>
 
* '''Porzellanpackung mit den Maßen: 11 cm hoch, 10 cm breit und 10 cm tief'''
 
* '''Porzellanpackung mit den Maßen: 11 cm hoch, 10 cm breit und 10 cm tief'''
 +
<br>
 
* '''Parfumpackung mit den Maßen: 8 cm hoch, 8 cm breit und 8 cm tief'''
 
* '''Parfumpackung mit den Maßen: 8 cm hoch, 8 cm breit und 8 cm tief'''
 +
<br>
 
* '''Spaghettipackung mit den Maßen: 24 cm hoch, 8 cm breit und 4 cm tief'''
 
* '''Spaghettipackung mit den Maßen: 24 cm hoch, 8 cm breit und 4 cm tief'''
 +
<br>
 
* '''Milchpackung mit den Maßen: 18 cm hoch, 10 cm breit und 6 cm tief'''
 
* '''Milchpackung mit den Maßen: 18 cm hoch, 10 cm breit und 6 cm tief'''
 +
<br>
 
* '''DVD-Packung mit den Maßen: 17 cm hoch, 14 cm breit und 3 cm tief'''
 
* '''DVD-Packung mit den Maßen: 17 cm hoch, 14 cm breit und 3 cm tief'''
 +
 
<br>
 
<br>
 
| [[Bild:Vergleich_Volumen.jpg|350px]]
 
| [[Bild:Vergleich_Volumen.jpg|350px]]

Version vom 14. Juli 2010, 21:29 Uhr

Inhaltsverzeichnis

Volumen von Würfel und Quader



Einheitswürfel



Wenn wir vom Volumen sprechen meinen wir den Rauminhalt. Rechts in dem Bild kannst du innerhalb des Würfels einen kleineren Würfel sehen. Diesen nennen wir den Einheitswürfel. Einheitswürfel heißt er, weil er 1 cm breit, 1 cm hoch und 1 cm tief ist. Somit können wir sein Volumen als 1 cm³ definieren.

V=1 cm^3

Wenn wir nun bei einem Körper das Volumen angeben möchten, dann brauchen wir einfach nur nachzuzählen wie viele Einheitswürfel da rein passen. Haben wir z.B. einen Würfel wo 27 Einheitswürfel reinpassen, dann haben wir ein Volumen von 27 m³.

Einheitswürfel.png






Aufgabe 1:Wie viele Würfel wurden gebraucht?

Für die Figur A wurden 16 (Würfel) benötigt. Das sind 4 (Würfel) mehr als bei Figur B. 29 (Würfel) braucht man um die Figur C zu erhalten. Um daraus ein Quader zu bekommen muss man noch 43 (Würfel) dazupacken.

AufgabeWürfel.png






Volumen vom Würfel



Da wir nicht immer alle Einheitswürfel abzählen können, brauchen wir eine Formel die uns beim Berechnen des Volumens helfen soll. Um diese zu erhalten sollen uns die zwei folgenden Bilder helfen.

Hier rechts im Bild haben wir vorne a Einheitswürfel nebeneinander liegen. Und diese Reihe haben wir nach hinten weg insgesamt a mal liegen.

Kannst du sagen wie groß dieses untere Volumen ist? (a·a cm³) (!a+a cm³) (!a cm³) (!2·a cm³)

Würfel1Einheitswürfel.png

Wir wissen nun, dass unser unteres Volumen a² m³ groß ist. Dieses Volumen haben wir, wie du rechts im Bild sehen kannst auch a mal nach oben hin.

Kannst du nun auch sagen wie groß dieses Volumen ist? (a²·a cm³) (!a²·a cm²) (!a²+a cm³) (!2·a² cm³)

Zähle bei dem Bild ab wie groß a ist. Kannst du sagen wie groß das Volumen an diesem speziellen Würfel ist? (!32 cm³) (!20 cm³)(!64 cm²) (64 cm³)

Würfel4Einheitswürfel.png






Volumen vom Quader



Die Einheitswürfel helfen uns nicht nur beim Würfel, sondern auch bei Quader. Hier müssen wir aber beachten, dass wir drei verschiedene Kantenlängen haben. Schaue dir dazu doch mal das Applet rechts an. Ziehst du an dem Punkt nach rechts, so füllt sich der Quader mit Einheitswürfeln.
Kannst du sagen, wie man das Volumen vom Quader berechnet? Schaue dir dazu nochmal die Schritte an, wie wir auf die Volumenformel beim Würfel gekommen sind.
Beachte:Gib das Rechenzeichen als Wort an, z.B. für "+" schreibst du "plus", für "·" schreibst du "mal".

Die Volumenformel für ein Quader lautet: V=a mal b mal c(Volumen vom Quader)






Übung 1: Verpackungen über Verpackungen



Ein großer Verpackungenhersteller muss die richtige Verpackung für ein neues Produkt finden und untersucht dafür bereits existierende Verpackungen. Die Verpackung muss groß genug sein, dass eine Füllung von 1 l reinpasst. Untersucht werden die folgenden Verpackungen (siehe auch rechts im Bild):

  • Porzellanpackung mit den Maßen: 11 cm hoch, 10 cm breit und 10 cm tief


  • Parfumpackung mit den Maßen: 8 cm hoch, 8 cm breit und 8 cm tief


  • Spaghettipackung mit den Maßen: 24 cm hoch, 8 cm breit und 4 cm tief


  • Milchpackung mit den Maßen: 18 cm hoch, 10 cm breit und 6 cm tief


  • DVD-Packung mit den Maßen: 17 cm hoch, 14 cm breit und 3 cm tief


Vergleich Volumen.jpg

Berechne bei allen Verpackungen die Füllmenge (mache die Nebenrechnungen auf ein extra Blatt Papier) und trage die Lösungen unten ein.Gebe die Füllmenge in ml an.
Beachte: 1 ml = 1 cm³

  • Porzellanpackung: 1100(ml)
  • Parfumpackung: 512(ml)
  • Spaghettipackung: 768(ml)
  • Milchpackung: 1080(ml)
  • DVD-Packung: 714(ml)


Die Hersteller benötigt eine Verpackung mit einer Füllmenge von mindestens 1 l, welche Verpackungen kommen dafür in Frage?
Beachte: 1 l = 1000 ml; es können mehrere Antworten richtig sein. (Porezellanpackung) (!Parfumpackung) (!Spaghettipackung) (Milchpackung) (!DVD-Packung)






Nuvola apps kig.png   Merke
Volumen von Würfel und Quader:
  • Das Volumen eines Würfels berechnest du mit
    V=a^3
    (Beachte: a steht für die Kantenlänge des Würfels, V steht für das Volumen.)


  • Das Volumen eines Quaders berechnest du mit
    V=a\cdot b\cdot c
    (Beachte: a, b und c stehen für die Kantenlängen des Quaders.)


Übertrage diesen Merksatz in die vorhergesehene Stelle auf deinem Arbeitsblatt.

Hier geht es zurück

Hier geht es zurück