2.Station: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Herleitung vereinfacht) |
K |
||
| Zeile 12: | Zeile 12: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
<math>\overline{ZA'} =</math> '''<math>|k| \cdot \overline{ZA}</math>''' <math>\wedge</math> <math>\overline{ZB'} =</math> '''<math>|k| \cdot \overline{ZB}</math>'''<br> | <math>\overline{ZA'} =</math> '''<math>|k| \cdot \overline{ZA}</math>''' <math>\wedge</math> <math>\overline{ZB'} =</math> '''<math>|k| \cdot \overline{ZB}</math>'''<br> | ||
| − | <math>\overline{AA'} = | + | <math>\overline{AA'} = \overline{ZA'} \cdot \overline{ZA} \wedge \overline{BB'} = \overline{ZB'} \cdot \overline{ZB}</math><br> |
| − | Einsetzen von <math>\overline{ZA'}</math> | + | Einsetzen der Formeln von <math>\overline{ZA'}</math> und <math>\overline{ZB'}</math>:<br> |
<math>\overline{AA'} =</math> '''<math>|k| \cdot \overline{ZA} - \overline{ZA}</math>''' <math>\wedge</math> <math>\overline{BB'} =</math> '''<math>|k| \cdot \overline{ZB} - \overline{ZB}</math>'''<br> | <math>\overline{AA'} =</math> '''<math>|k| \cdot \overline{ZA} - \overline{ZA}</math>''' <math>\wedge</math> <math>\overline{BB'} =</math> '''<math>|k| \cdot \overline{ZB} - \overline{ZB}</math>'''<br> | ||
Aufgelöst nach |k|:<br> | Aufgelöst nach |k|:<br> | ||
Version vom 7. Juli 2009, 18:17 Uhr
1. Station: Erster Vierstreckensatz - Schenkellösung - 2. Station: Erster Vierstreckensatz - Abschnittlösung - 3. Station: Zweiter Vierstreckensatz - 4. Station: Zusammenfassung - 5. Station: Übung
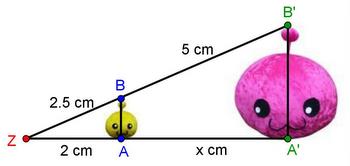
2. Station: Erster Vierstreckensatz - Abschnittlösung
- Bei dieser Aufgabe sollst du berechnen, wie weit Dia von Panto entfernt ist. Die gesuchte Größe ist hier nur ein
- Abschnitt des Schenkels.
- Anhand der Eigenschaft der Längenverhältnisstreue der zentrischen Streckung, kannst du auch hier wieder die geeignete Formel
- zur Berechnung der unbekannten Strecke herleiten. Setze dafür die richtige Aussage in die passende Lücke ein:
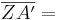
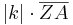
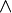
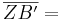
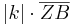
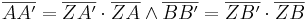
Einsetzen der Formeln von 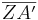 und
und 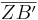 :
:
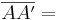
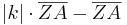
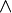
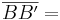
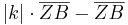
Aufgelöst nach |k|:
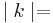
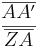
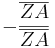
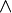
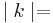
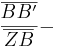
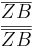
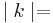
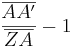
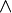
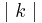
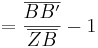
Gleichsetzen:
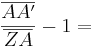
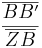
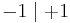
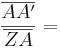
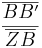
- Super! Du hast die Abschnittlösung des ersten Vierstreckensatzes hergeleitet.
- Auch hier verhalten sich die Abschnitte auf der einen Halbgeraden, wie die Abschnitte auf der anderen Halbgeraden.
- Berechne nun die Aufgabe in deinem Heft und trage hier deine Lösung mit Angabe der Einheit (cm) ein!
x = 4 cm (Tipp: Leerzeichen zwischen Zahl und Einheit nicht vergessen!).