Die Normalparabel stellt sich vor: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(kurze Einführung zur Normalparabel)
(Station 2 erweitert... Entdecken der Normalparabel)
Zeile 57: Zeile 57:
  
 
<div align="center"><big><u>'''STATION 2: Die Normalparabel als Funktionsvorschrift'''</u></big></div>
 
<div align="center"><big><u>'''STATION 2: Die Normalparabel als Funktionsvorschrift'''</u></big></div>
 +
 +
[[Bild: Normalparabel-Wertetabelle.jpg|thumb|right|Normalparabel]]
 +
 +
 +
'''Aufgabe:''' 
 +
 +
In der aufgeführten Normalparabel kannst du die Punkte zum erstellen einer Wertetabelle erkennen.
 +
 +
a) Nehme ein Blatt Papier und suche für die folgenden x-Werte die zugehörigen y-Werte und stelle eine Wertetabelle auf für:
 +
 +
* x<sub>1</sub> = 1
 +
* x<sub>2</sub> = -1
 +
* x<sub>3</sub> = 2
 +
* x<sub>4</sub> = -2
 +
* x<sub>5</sub> = 3
 +
* x<sub>6</sub> = -3
 +
 +
 +
{{Lösung versteckt|
 +
[[Bild: Wertetabelle.jpg|Normalparabel]]
 +
}}
 +
 +
 +
b) Was fällt dir beim y-Wert im Bezug zum x-Wert auf?
 +
 +
'''Hilfe:'''
 +
{{versteckt|
 +
Eine Aussage stimmt!
 +
* Der y-Wert ist immer das doppelte des x-Wertes: f(x)<math>=</math>2x
 +
* Der x-Wert und der y-Wert stehen in keinem Zusammenhang
 +
* Der y-Wert entsteht aus dem Quadrat des x-Wertes: f(x)<math>=</math>x<sup>2</sup> }}
 +
 +
{{Lösung versteckt|
 +
Der y-Wert ist immer das Quadrat des x-Wertes: f(x)<math>=</math>x<sup>2</sup>}}

Version vom 9. Juli 2009, 15:22 Uhr

Mathematik-digital Pfeil-3d.png
Lernpfad

Die Normalparabel stellt sich vor


Auf dieser Seite lernst du die einfachste Form der quadratischen Funktion! Bearbeite den unten aufgeführten Lernpfad

  • Entdecken der Normalparabel
  • Die Normalparabel als Funktionsvorschrift
  • Eigenschaften der Normalparabel erkunden
  • Besondere Eigenschaft der Normalparabel


Auf gehts:

Eine neue Klasse von Funktionen stellt sich vor!

Hast du schon mal was von der Parabel gehört?


Vielleicht kennst du ja schon die Parabel, falls nicht, versuche durch Zuordnung die Normalparabel zu entdecken.


Tipps:

- Zwei der drei dargestellten Grafiken müssten dir bekannt sein!

- Ziehe die vorgegebenen Lösungen zur richtigen Grafik durch festhalten der linken Maustaste



STATION 1: Entdecken der Normalparabel


Datei:Normalparabel.jpg Normalparabel
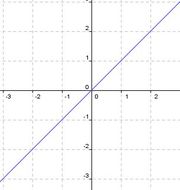Lineare-Funktion.jpg Lineare Funktion
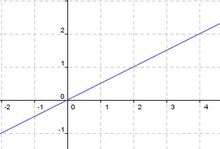F(x)=0,5x.jpg f(x)= 0,5x


Super! Nun weißt du wie die Parabel aussieht, wenn du es nicht schon längst gewusst hast.

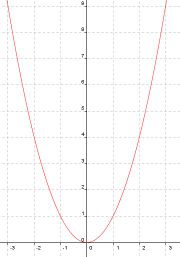
Wie du dir sicher denken kannst, kann man die Normalparabel auch als Funktion darstellen.

Dafür wollen wir eine Wertetabelle erstellen.



STATION 2: Die Normalparabel als Funktionsvorschrift
Normalparabel


Aufgabe:

In der aufgeführten Normalparabel kannst du die Punkte zum erstellen einer Wertetabelle erkennen.

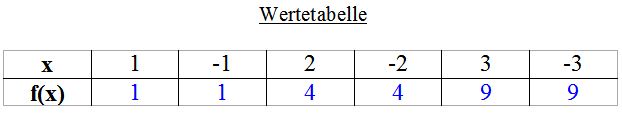
a) Nehme ein Blatt Papier und suche für die folgenden x-Werte die zugehörigen y-Werte und stelle eine Wertetabelle auf für:

  • x1 = 1
  • x2 = -1
  • x3 = 2
  • x4 = -2
  • x5 = 3
  • x6 = -3


Normalparabel


b) Was fällt dir beim y-Wert im Bezug zum x-Wert auf?

Hilfe:

Eine Aussage stimmt!

  • Der y-Wert ist immer das doppelte des x-Wertes: f(x)=2x
  • Der x-Wert und der y-Wert stehen in keinem Zusammenhang
  • Der y-Wert entsteht aus dem Quadrat des x-Wertes: f(x)=x2

Der y-Wert ist immer das Quadrat des x-Wertes: f(x)=x2
Von „http://dmuw.zum.de/index.php?title=Lernpfade/Quadratische_Funktionen/Die_Normalparabel_stellt_sich_vor&oldid=2611“