Mathematisches Modellieren: Unterschied zwischen den Versionen
(→Beispielaufgabe: Außenputz) |
|||
| Zeile 1: | Zeile 1: | ||
| − | + | = Beispielaufgabe: Außenputz = | |
| + | |||
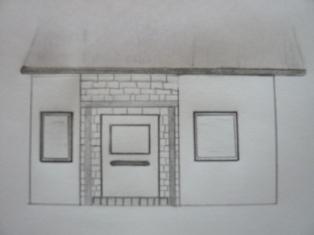
| + | Das abgebildete Haus soll verputz werden. Vom Dach bis zur Unterseite des Balkons wird das Haus allerdings mit Holz verkleidet. | ||
| + | [[Bild:Haus]] | ||
== Modellierungskreislauf == | == Modellierungskreislauf == | ||
Version vom 21. September 2010, 21:37 Uhr
Inhaltsverzeichnis |
Beispielaufgabe: Außenputz
Das abgebildete Haus soll verputz werden. Vom Dach bis zur Unterseite des Balkons wird das Haus allerdings mit Holz verkleidet. Datei:Haus
Modellierungskreislauf
Aufgabe verstehen
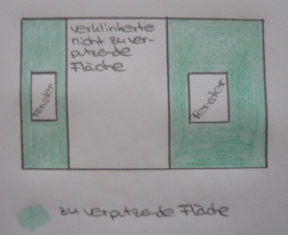
Zunächst mache ich mir eine Vorstellung darüber, wie die zu verputzende Wand später aussehen soll und fertige dazu eine Skizze an
Nun überlege ich welche Teile der Wand verputzt werden sollen bzw. nicht verputzt werden sollen. Ich muss also von der kompletten Wandfläche folgende Flächen abziehen:
- kleines Fenster
- großes Fenster
- verklinkerte Fläche um die Haustüre
Ich habe nun also eine genaue Vorstellung von der Aufgabe.
Aber wie berechne ich nun die gesuchte Fläche?
Modell erstellen
Um die Flächen berechnen zu können überlege ich welche mathematische Formen, deren Flächeninhalt ich berechene kann, die Wand am besten beschreiben. Für die einzelnen Wandflächen und Fenster sind Rechtecke am naheliegensten. SOmit ergibt sich folgende Skizze:
Aber wie soll ich die Fläche ohne Längenangaben berechnen?
Ich betrachte nochmals das Bild in der Angabe! Ich weiß, dass eine normale Raumhöhe etwa 2,60m entspricht. Also nehme ich diesen Wert von 2,60m für die Raumhöhe des Hauses an und messe diese im Bild. Dies ist gut möglich, da man zwischen den einzelnen Mauersteinen die Decke gut erkennen kann. Ich messe hier 2,7cm. Der Rest des Hauses wird auch noch vermessen.
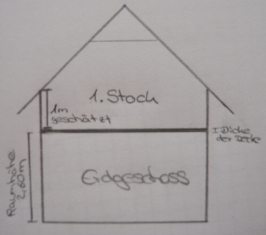
Für die Breite der Wand reicht mir die Höhe des Raumes allerdings noch nicht. Also messe ich die Dicke der Decke nach. Hier ergibt sich der Wert 0,25cm. Nun fehlt aber immernoch ein Stück, das ich aber nicht messen kann, da ein Teil der Wand vom Dachvorsprung verdeckt wird. Dieses Stück entspricht im Zimmer des 1. Stocks dem senkrechten Teil der Wand, der bis zu Beginn der Dachschräge reicht. Zur Veranschaulichung hier eine kleine Skizze:
Da ich schon oft in einem solchen Zimmer war, kann ich diese Höhe gut schätzen. Ich nehme hierfür 1m an.
Mathematik benutzen
Mit Hilfe des Dreisatzes kann ich nun die im Bild gemessenen Maße in die entsprechenden realen Längen umrechnen
2,7cm: 2,6m
1cm: 0,96m
Haus:
Länge: 7,3cm: 7m
Breite: 0,25cm: 0,24m → 2,6m+0,24m+1m=3,84m
Breite linker Wandabschnitt: 1,3cm: 1,25m
Breite rechter Wandabschnitt: 3cm: 2,88m
großes Fenster:
Breite: 1,1cm: 1,06m
Länge: 1,5cm: 1,44m
kleines Fenster:
Breite: 0,7cm: 0,67m
Länge: 1,5cm: 1,44m
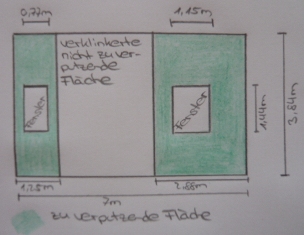
Nun kann ich die Maße in meine Skizze eintragen:
Da ich nun alle nötigen Maße habe, kann ich mit der Flächenberechnung beginnen:
Flächenberechnung: (linke Wandfläche + rechte Wandfläche) - (kleines Fenster + großes Fenster)
Zu Berechnen ist somit folgender Term:
(1,25m · 3,84m + 2,88m · 3,84m) - (0,67m · 1,44m + 1,06m · 1,44m)
= (4,80m² + 11,06m²) - (0,96m² + 1,53m²)
= 15,86m² - 2,49m²
= 13,37m²