The tidiness of elementary mathematics: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „We all expect a certain { tidiness} to mathematics, and for many this provides a gratifying aesthetic pleasure. However, there are some wrinkles. One of these ari…“)
 
Zeile 1: Zeile 1:
−
We all expect a certain { tidiness} to mathematics, and for many this provides a gratifying aesthetic pleasure. However, there are some wrinkles. One of these arises in the integral of <math>x^k</math>. Calculus provides us with the formula <math>\label{eq:int_xk}
+
We all expect a certain tidiness to mathematics, and for many this provides a gratifying aesthetic pleasure. However, there are some wrinkles. One of these arises in the integral of <math>x^k</math>. Calculus provides us with the formula <math>
 
     \int x^k\mathrm{d}x = \frac{x^{k+1}}{k+1}.
 
     \int x^k\mathrm{d}x = \frac{x^{k+1}}{k+1}.
 
</math> However, this equation is only correct for <math>k\neq -1</math>. If we try to take <math>k=-1</math> the right hand side is meaningless because we have a zero on the denominator of the fraction, i.e. <math>\frac{1}{0}</math>. But in this case a separate argument gives the answer <math>\label{eq:int_log}
 
</math> However, this equation is only correct for <math>k\neq -1</math>. If we try to take <math>k=-1</math> the right hand side is meaningless because we have a zero on the denominator of the fraction, i.e. <math>\frac{1}{0}</math>. But in this case a separate argument gives the answer <math>\label{eq:int_log}
Zeile 5: Zeile 5:
 
</math> Our expectation is that these two formulae should be reconciled. Indeed, if we let <math>k</math> approach <math>-1</math> in the first we should end up with the second, but that fails to happen. For each <math>x</math>, <math>\lim_{k\rightarrow -1} \frac{x^{k+1}}{k+1} </math> is undefined. You can try this on the graph below.
 
</math> Our expectation is that these two formulae should be reconciled. Indeed, if we let <math>k</math> approach <math>-1</math> in the first we should end up with the second, but that fails to happen. For each <math>x</math>, <math>\lim_{k\rightarrow -1} \frac{x^{k+1}}{k+1} </math> is undefined. You can try this on the graph below.
  
−
This is particularly problematic when we attempt to automate knowledge, that is when we seek to devise a { computer algebra system} which will symbolically manipulate expressions. If we want to integrate <math>x^{k}</math> with respect to <math>x</math> we certainly have two choices
+
== Main article ==
−
 
+
−
# Ignore the special case <math>k=1</math>.
+
−
# Ask the user if <math>k=-1</math>.
+
−
 
+
−
Both of these approaches are problematic. <math>k=-1</math> is only one point out of an infinity of other values for <math>k</math>. However, in mathematics such exceptional cases occur rather more often than you might expect if you just stuck a pin in the number line, or even if you chose an integer <math>k</math> at random. Asking the user can also be problematic as they many not yet know the value of <math>k</math>, or the integral might occur deep within some other function and the user may have no idea what the question is asking! Automatically using the formula  might result in an error creeping into a much longer calculation. Mistakes like this are very hard to track down and can be serious.
+
−
 
+
−
What we would really like is a formula that works for all <math>k</math>. Here we are going to consider the comment in  that really, at a symbolic level, the answer to <math>\int x^k\mathrm{d}x </math> might better be written as <math>\label{eq:int_xk2}
+
−
    \int x^k\mathrm{d}x = \frac{x^{k+1}-1}{k+1}+c.
+
−
</math>
+
−
 
+
−
First consider the (easy) case <math>k\neq -1</math>. If we fix <math>k</math> and differentiate then we obtain <math>\frac{\mathrm{d}}{\mathrm{d}x}\frac{x^{k+1}-1}{k+1} = x^k.</math> So <math>\frac{x^{k+1}-1}{k+1}=\frac{x^{k+1}}{k+1}-\frac{1}{k+1}</math> is an anti-derivative of <math>x^k</math>. Really we have chosen a slightly different constant of integration.
+
−
 
+
−
Whereas we originally had the form <math>\frac{x^{0}}{0}=\frac{1}{0}</math>, the new formula gives <math>\frac{x^{0}-1}{0}=\frac{0}{0}</math>. To understand what is going on we need to look at this expression for <math>k</math> close to <math>-1</math> and take a { limit}, i.e.  <math>\lim_{k\rightarrow -1} \frac{x^{k+1}-1}{k+1}.</math> If we can make sense of this limit, then we will define the value of the expression at <math>k=-1</math> by the value of the limit, thus removing the exceptional case in a meaningful way. This sort of thing is a standard mathematician&rsquo;s move.
+

Version vom 8. November 2011, 23:17 Uhr

We all expect a certain tidiness to mathematics, and for many this provides a gratifying aesthetic pleasure. However, there are some wrinkles. One of these arises in the integral of 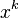x^k. Calculus provides us with the formula 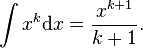\int x^k\mathrm{d}x = \frac{x^{k+1}}{k+1}. However, this equation is only correct for 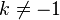k\neq -1. If we try to take 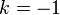k=-1 the right hand side is meaningless because we have a zero on the denominator of the fraction, i.e. \frac{1}{0}. But in this case a separate argument gives the answer Fehler beim Parsen(Unbekannte Funktion „\label“): \label{eq:int_log} \int x^{-1}\mathrm{d}x = \int \frac{1}{x}\mathrm{d}x = \ln(x).%\ln(|x|). 

Our expectation is that these two formulae should be reconciled. Indeed, if we let k approach -1 in the first we should end up with the second, but that fails to happen. For each x, \lim_{k\rightarrow -1} \frac{x^{k+1}}{k+1}  is undefined. You can try this on the graph below.

Main article

Von „http://dmuw.zum.de/index.php?title=The_tidiness_of_elementary_mathematics&oldid=30218“