Flächeninhalt Parallelogramm: Unterschied zwischen den Versionen
(Tabelle geändert, Frage eingefügt) |
(Bild eingefügt) |
||
| Zeile 4: | Zeile 4: | ||
[[Bild:Ebert_MotivatorParallelogramm.jpg|center]] | [[Bild:Ebert_MotivatorParallelogramm.jpg|center]] | ||
<br> | <br> | ||
| − | :'''Lass uns hier gemeinsam die Formel für den Flächeninhalt des Parallelogramms erarbeiten. Du wirst sehen, es ist gar nicht so schwer!''' | + | :'''''Lass uns hier gemeinsam die Formel für den Flächeninhalt des Parallelogramms erarbeiten. Du wirst sehen, es ist gar nicht so schwer!''''' |
| − | : '''Hier siehst Du eine Möglichkeit, wie man die Flächeninhaltsformel von Parallelogrammen herleiten kann ''' | + | |
| + | ---- | ||
| + | |||
| + | : '''''Hier siehst Du eine Möglichkeit, wie man die Flächeninhaltsformel von Parallelogrammen herleiten kann ''''' | ||
<br> | <br> | ||
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
{| <br> | {| <br> | ||
| − | '''Verschiebe das Dreieck und beobachte was passiert!''' '''Bearbeite dazu die nebenstehenden Fragen''': | + | '''''Verschiebe das Dreieck und beobachte was passiert!''' '''Bearbeite dazu die nebenstehenden Fragen''':'' |
| <ggb_applet height="400" width="400" showResetIcon="true" filename="Ebert_parallelogrammverschieben2.ggb" />|| | | <ggb_applet height="400" width="400" showResetIcon="true" filename="Ebert_parallelogrammverschieben2.ggb" />|| | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 18: | Zeile 21: | ||
</quiz> | </quiz> | ||
<br> | <br> | ||
| − | '''2.''' '''Begründe, warum ein Rechteck ensteht''' <br> | + | '''2.''' '''Begründe, warum ein ''Rechteck'' ensteht''' <br> |
| − | '''Tipp: Denke an die Innenwinkelsumme im Dreieck und Paralellogramm! Lasse Dir dazu die Winkel anzeigen. | + | '''Tipp:''' {{ versteckt| Denke an die Innenwinkelsumme im Dreieck und Paralellogramm! Lasse Dir dazu die Winkel anzeigen.}}<br> |
*Bearbeite dazu den folgenden Lückentext: | *Bearbeite dazu den folgenden Lückentext: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 35: | Zeile 38: | ||
<br> | <br> | ||
|- | |- | ||
| − | |'''3. Welche Breite besitzt das Rechteck? ''' | + | |'''3. Welche ''Breite'' besitzt das Rechteck? ''' |
<quiz display="simple"> | <quiz display="simple"> | ||
{Markiere die richtige Antwort} | {Markiere die richtige Antwort} | ||
| Zeile 44: | Zeile 47: | ||
</quiz> | </quiz> | ||
| − | * '''Berechne den Flächeninhalt des Rechtecks. <br> In der Darstellung entspricht ein Kästchen einem Zentimeter. | + | * '''Berechne den ''Flächeninhalt des Rechtecks''. '''<br> Hinweis: {{versteckt|In der Darstellung entspricht ein Kästchen einem Zentimeter.}} |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Der Flächeninhalt des Rechtecks beträgt '''12 (cm²)'''<br> | Der Flächeninhalt des Rechtecks beträgt '''12 (cm²)'''<br> | ||
| Zeile 54: | Zeile 57: | ||
|} | |} | ||
</div> | </div> | ||
| − | + | [[Bild:Ebert_MotivatorGrün.jpg|100px|right]] | |
| + | '''''Wie war das doch?''''' | ||
<br> | <br> | ||
| + | '''''Maja hat sich nicht alles gemerkt'''''. <br> | ||
| + | <br> | ||
| + | '''''Nils hat ihr die Herleitungsidee nochmals zusammengefasst''':'' | ||
<br> | <br> | ||
<br> | <br> | ||
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
{| | {| | ||
| − | | [[Bild:Ebert_MotivatorMerke.jpg]] || | + | | [[Bild:Ebert_MotivatorMerke.jpg|200px]] || |
| − | *Wir haben das Parallelogramm in ein '''Trapez''' und ein '''rechtwinkliges Dreieck''' zerlegt. | + | *Wir haben das '''Parallelogramm''' in ein '''Trapez''' und ein '''rechtwinkliges Dreieck''' zerlegt. |
*Anschließend wurd das Trapez durch '''Verschiebung''' des '''Dreiecks zum Rechteck ergänzt'''. Diese Verschiebung stellt eine '''Kongruenzabbildung''' dar. <br> | *Anschließend wurd das Trapez durch '''Verschiebung''' des '''Dreiecks zum Rechteck ergänzt'''. Diese Verschiebung stellt eine '''Kongruenzabbildung''' dar. <br> | ||
*Das erhaltene Rechteck und das Ausgangsdreieck sind damit '''zerlegungsgleich''' und besitzen somit den '''gleichen Flächeninhalt'''. | *Das erhaltene Rechteck und das Ausgangsdreieck sind damit '''zerlegungsgleich''' und besitzen somit den '''gleichen Flächeninhalt'''. | ||
<br> | <br> | ||
<br> | <br> | ||
| − | Da diese Zerlegung und Ergänzung für alle Parallelogramme umsetzbar ist, können wir die Flächeninhaltsformel für Parallelogramme auf die Formel für Rechtecke zurückführen. | + | '''Da diese Zerlegung und Ergänzung für alle Parallelogramme umsetzbar ist, können wir die Flächeninhaltsformel für Parallelogramme auf die Formel für Rechtecke zurückführen.''' |
|} | |} | ||
</div> | </div> | ||
| Zeile 72: | Zeile 79: | ||
---- | ---- | ||
| − | + | [[Bild:Ebert_Motivatoren.jpg|150px]]<br> | |
| + | '''''Maja:''''' ''' <span style="color: green">"Ah, ich habe es jetzt verstanden! Ich zerlege das Parallelogramm und ergänze zum Rechteck. Denn von Rechtecken kann ich den Flächeninhalt ganz leicht über die Formel ''Länge mal Breite'' berechnen.<br> Die Länge des Rechtecks entspricht dabei der Grundseite des Parallelogramms. Doch wie war das mit der Breite im Parallelogramm??"</span>''' | ||
| + | <br> | ||
| + | '''''Nils:''''' '''<span style="color: red">"Das zeige ich Dir auf der folgenden Seite"</span>'''<br> | ||
<br> | <br> | ||
| − | '''Hier geht es weiter zum nächsten Abschnitt:'''<br> | + | '''''Hier geht es weiter zum nächsten Abschnitt:'''''<br> |
| − | [[Höhen im Parallelogramm]] | + | →[[Höhen im Parallelogramm]] |
Version vom 16. Juli 2009, 09:03 Uhr
Flächeninhalt Parallelogramm
Einstieg
- Lass uns hier gemeinsam die Formel für den Flächeninhalt des Parallelogramms erarbeiten. Du wirst sehen, es ist gar nicht so schwer!
- Hier siehst Du eine Möglichkeit, wie man die Flächeninhaltsformel von Parallelogrammen herleiten kann
|
Denke an die Innenwinkelsumme im Dreieck und Paralellogramm! Lasse Dir dazu die Winkel anzeigen.
| |
| 3. Welche Breite besitzt das Rechteck?
In der Darstellung entspricht ein Kästchen einem Zentimeter.
Der Flächeninhalt des Rechtecks beträgt 12 (cm²)
|
Wie war das doch?
Maja hat sich nicht alles gemerkt.
Nils hat ihr die Herleitungsidee nochmals zusammengefasst:

Maja: "Ah, ich habe es jetzt verstanden! Ich zerlege das Parallelogramm und ergänze zum Rechteck. Denn von Rechtecken kann ich den Flächeninhalt ganz leicht über die Formel Länge mal Breite berechnen.
Die Länge des Rechtecks entspricht dabei der Grundseite des Parallelogramms. Doch wie war das mit der Breite im Parallelogramm??"
Nils: "Das zeige ich Dir auf der folgenden Seite"
Hier geht es weiter zum nächsten Abschnitt:
→Höhen im Parallelogramm

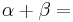 180°
180°
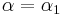
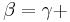 90° bzw.
90° bzw.
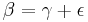
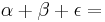 180°
180°

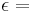 90° und
90° und 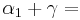 90°
90°



