Flächeninhalt ebener Figuren: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(→Das solltest Du wissen: Formel mit Erklärung eingefügt) |
(→Das solltest Du wissen: Applets eingefügt und Merkkasten in Tabellenform) |
||
| Zeile 45: | Zeile 45: | ||
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
{| <br> | {| <br> | ||
| − | + | [[Bild:Ebert_MotivatorMerke.jpg|100px|left]]'''''Variiere die Seitenlängen des Rechtecks und des Quadrates an den farbigen Eckpunkten. Wie ändert sich der Flächeninhalt?''''' | |
| − | + | {| class="prettytable" | |
| + | |- | ||
| + | | <ggb_applet height="400" width="500" showResetIcon="true" filename="Ebert_Rechteck.ggb"/> || <ggb_applet height="400" width="500" showResetIcon="true" filename="Ebert_Quadrat.ggb"/> | ||
| + | |- | ||
| + | | <u>Den <span style="color: red">'''Flächeninhalt von Rechtecken'''</span> berechnet man durch die Formel:</u><br> | ||
::::<math>F_{Rechteck}= g \cdot b</math> | ::::<math>F_{Rechteck}= g \cdot b</math> | ||
<br> | <br> | ||
| − | :mit <span style="color: red">'''g'''</span> als <span style="color: red">'''Länge der Grundseite'''</span> und <span style="color: red">'''b als Breite'''</span> des Rechtecks | + | :mit <span style="color: red">'''g'''</span> als <span style="color: red">'''Länge der Grundseite'''</span> und <span style="color: red">'''b als Breite'''</span> des Rechtecks |
| − | + | || | |
| − | + | <u>Ebenso berechnet man den <span style="color: red">'''Flächeninhalt von Quadraten'''</span>:</u> | |
| − | + | ||
::::<math>F_{Quadrat} = g\cdot b </math> <br> | ::::<math>F_{Quadrat} = g\cdot b </math> <br> | ||
::::Doch <span style="color: red">'''im Quadrat sind die Seiten b und g gleich lang'''</span>! <br> | ::::Doch <span style="color: red">'''im Quadrat sind die Seiten b und g gleich lang'''</span>! <br> | ||
::::Das heißt wir können schreiben: <br> | ::::Das heißt wir können schreiben: <br> | ||
:::<math>F_{Quadrat} = g\cdot g = g^2</math> <math>oder</math> <math>F_{Quadrat} = b\cdot b = b^2</math>. <br> | :::<math>F_{Quadrat} = g\cdot g = g^2</math> <math>oder</math> <math>F_{Quadrat} = b\cdot b = b^2</math>. <br> | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | |||
Version vom 24. Juli 2009, 17:31 Uhr
1.Wiederholung: Flächeninhalt von Rechtecken und Quadraten
- Entdecke auf dieser Seite, wie man die Flächeninhalte ebener Figuren berechnet!!
- Du hast bereits gelernt, wie man den Flächeninhalt von Rechtecken und Quadraten berechnet.
- Erinnerst Du Dich noch daran?
- Teste Dich in der nächsten Aufgabe. Berechne die fehlenden Felder und fülle die Lücken mit der passenden Antwort aus.
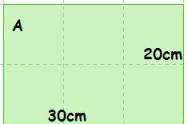30cm 
20cm = 600cm2
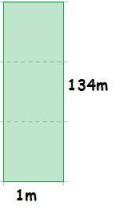1m 134m = 134m 2
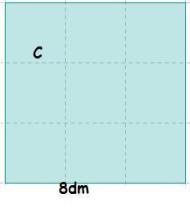8dm 8dm = 64dm 2
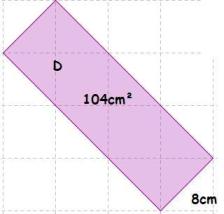8cm 13cm = 104cm2
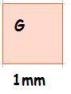1mm 1mm= 1mm2
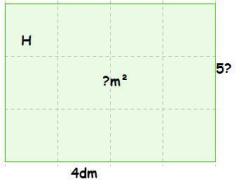4dm 5m = 2m2
a b = ab
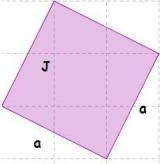a a = a2
- Du hast alle Aufgabe richtig gelöst? Sehr gut!
- Dann kennst Du noch die Flächeninhaltsformel für Rechtecke und Quadrate.
- Überprüfe im nächsten Abschnitt, ob du richtig liegst.
Das solltest Du wissen
- Merke Dir die Berechnung für die Flächeninhalte des Rechtecks und Quadrates gut! Du wirst sie später wieder gebrauchen.
| Den Flächeninhalt von Rechtecken berechnet man durch die Formel:
|
Ebenso berechnet man den Flächeninhalt von Quadraten:
|
.
Das war doch ganz leicht,oder?
Konzentrier Dich im nächsten Abschnitt gut, denn da lernst Du wieder etwas Neues.
Hier geht es weiter zum nächsten Abschnitt:
→Flächeninhalt Parallelogramm
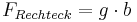
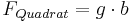
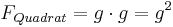
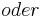
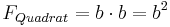