Grundlagen der Zerlegungsgleichheit von Figuren: Unterschied zwischen den Versionen
(Bilder eingefügt) |
K |
||
| Zeile 75: | Zeile 75: | ||
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
{| | {| | ||
| − | '''Merke''' | + | '''Merke''' <span style="color:#ff0000">'''Zerlegungsgleichheit von Figuren'''</span> |
| − | |Zwei Figuren sind <span style="color:#ff0000">'''zerlegungsgleich,'''</span> wenn sie in paarweise <span style="color:#ff0000">'''kongruente Teilfiguren'''</span> zerlegt werden können.<br> Beispiel: | + | |Zwei Figuren sind <span style="color:#ff0000">'''zerlegungsgleich,'''</span> wenn sie in paarweise <span style="color:#ff0000">'''kongruente Teilfiguren'''</span> zerlegt werden können.<br> ''Beispiel:'' |
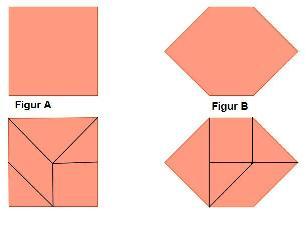
<br> [[Bild:Ebert_Merkbilder_Zerlegungsgleichheit.jpg]] | <br> [[Bild:Ebert_Merkbilder_Zerlegungsgleichheit.jpg]] | ||
<br> Figur A und Figur B sind zerlegungsgleich. Zerlegungsgleiche Figuren besitzen den gleichen <span style="color:#ff0000">'''Flächeninhalt'''</span> | <br> Figur A und Figur B sind zerlegungsgleich. Zerlegungsgleiche Figuren besitzen den gleichen <span style="color:#ff0000">'''Flächeninhalt'''</span> | ||
|} | |} | ||
</div> | </div> | ||
Version vom 4. Juni 2009, 10:48 Uhr
Auf dieser Seite lernst Du die Eigenschaften der Zerlegungsgleichheit von Figuren kennen.
Inhaltsverzeichnis |
Grundlagen der Zerlegungsgleichheit von Figuren
Wiederholung des Kongruenzbegriffes
Weißt Du noch was man unter Kongruenz von Figuren versteht??
Eine Wiederholung kann nicht schaden, oder?
Los geht´s: Teste Dein Wissen!
Ein anderes Wort für Kongruenz ist Deckungsgleichheit
Aufgabe: Wie erzeugt man kongruente Figuren?
Aufgabe: Kongruente Dreiecke
Findest Du alle Dreiecke, die zum Dreieck A kongruent sind?
Gib die Buchstaben an und begründe warum.
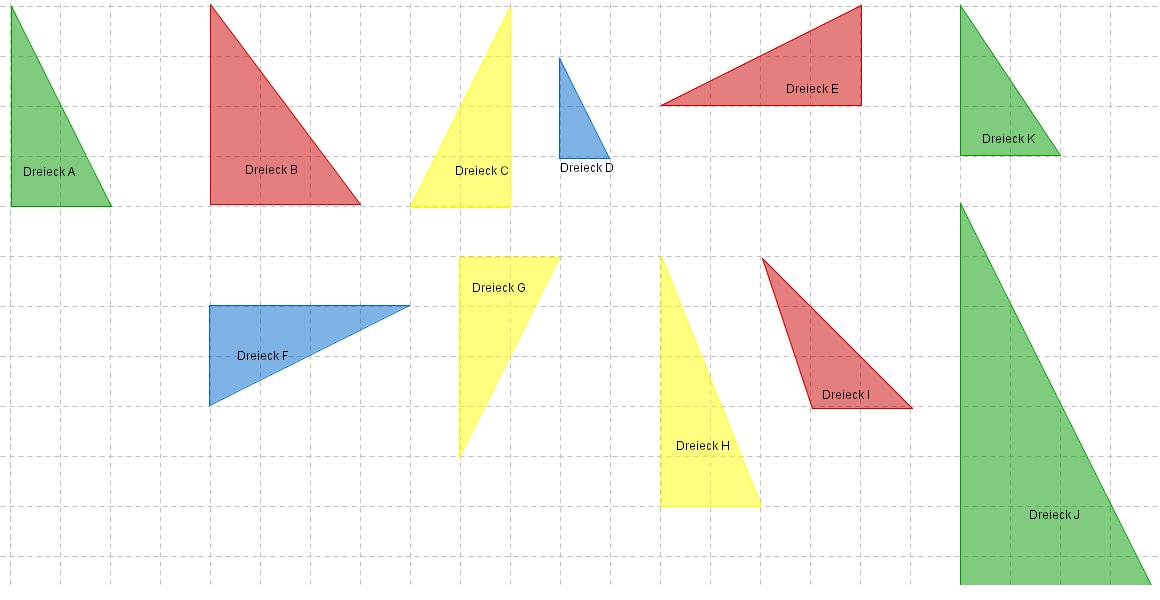
Lösung:
Kongruente Dreiecke zu A sind: E,F (Drehung); C(Spiegelung);G(Drehung und Spiegelung)
Welche Dreiecke sind ähnlich zu A??
Antwort:C,D,E,F,G,J sind ähnlich zu A
Kleines Quiz
Achtung!! Mehrere Antworten sind möglich!
Das sollest du also wissen
| Zwei Figuren sind zueinander kongruent, wenn sie durch Verschiebung,Drehung oder Spiegelung ineinander überführt werden können. Diese drei Abbildungen nennt man daher auch Kongruenz-abbildungen. |
Wofür können wir die Kongruenz von Figuren gebrauchen?
Du kennst sicher ein paar Anwendungsbeispiele wofür man die Eigenschaften der
Kongruenz von Figuren nutzen kann. (wird evt. später noch eingefügt: Kongruenz von Dreiecken, Konstruktionen)
Im nächsten Abschnitt lernst Du ein weiteres Anwendungsbeispiel kennen
Zerlegungsgleichheit von Figuren
Logbucheintrag
- Übertrage folgende Definition in Dein Heft:
| Zwei Figuren sind zerlegungsgleich, wenn sie in paarweise kongruente Teilfiguren zerlegt werden können. Beispiel:
|
