Berechnungen von Wahrscheinlichkeiten und relative Häufigkeit: Unterschied zwischen den Versionen
K |
K |
||
| Zeile 105: | Zeile 105: | ||
</div> | </div> | ||
| + | |||
| + | :: b) Ist es besser als Erster oder als Zweiter einen Würfel auszuwählen? <br /> Um diese Frage zu beantworten hilft dir das Wissen aus Teilaufgabe a). | ||
| + | |||
| + | <div class="multiplechoice-quiz"> | ||
| + | |||
| + | (!Es ist besser als Erster zu wählen) (Es ist besser als Zweiter zu wählen) | ||
| + | |||
| + | </div> | ||
| + | |||
| + | [[kurze Erklärung]] | ||
<div align="left">[[Benutzer:Annalena Dürr|<math>\Leftarrow</math> Zurück]]</div> | <div align="left">[[Benutzer:Annalena Dürr|<math>\Leftarrow</math> Zurück]]</div> | ||
Version vom 24. September 2009, 17:00 Uhr
Aufgabe 1:
- Das nachstehende Kreuzworträtsel soll dir helfen, dich an einige Begriffe zu erinnern.
- Beim Klick auf die Ziffern im Kreuzworträtsel öffnet sich ein Eingabefeld zum Eintragen.
| absolute | Bei 100maligen Würfeln wird 18 mal eine 6 gewürfelt. 18 bezeichnet man dann als ... Häufigkeit. |
| relative | Bei 100maligen Würfeln wird 18 mal eine 6 gewürfelt. Den Quotienten aus 6 und 18 bezeichnet man dann als ... Häufigkeit. |
| Ergebnis | Jeder mögliche Ausgang eines Zufallsexperimentes heißt ...? |
| Ergebnisraum | Die Menge aller Ergebnisse heißt...? |
| Ereignis | Es wird ein klassischer Würfel geworfen und anschließend darauf geachtet, ob die Augenzahl gerade ist. "Augenzahl gerade" wird als ... bezeichnet. |
| Ereignisraum | Die Menge aller Ereignisse bezeichnet man als ... |
| Laplace | Beim Würfeln ist es gleich wahrscheinlich eine 1; 2; 3; 4; 5 oder 6 zu erhalten. Solche Experimente werden als ...-Experiment bezeichnet. |
Aufgabe 2:
- Die relative Häufigkeit lässt sich durch den Quotienten
bestimmen.
- Die relative Häufigkeit lässt sich durch den Quotienten
- a) In diesem Triplett findest du zusammengehörende relative Häufigkeiten als Bruch, Dezimalzahl und Prozentangabe.
Finde diese Triplette:
- a) In diesem Triplett findest du zusammengehörende relative Häufigkeiten als Bruch, Dezimalzahl und Prozentangabe.
 |
 |
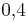40% |
 |
 |
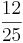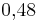48% |
 |
 |
 %
|
 |
 |
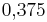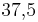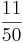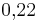22% |
 |
 |
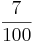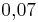7% |
 |
 |
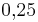25% |
 |
 |
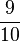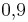90% |
- b) Berechne zu den nachfolgenden Experimenten die relative Häufigkeit. Kreuze die richtige Antwort an.
Es können auch mehrere Antworten richtig sein.
- b) Berechne zu den nachfolgenden Experimenten die relative Häufigkeit. Kreuze die richtige Antwort an.
Es wird 20mal gewürfelt, davon fällt 5 mal eine 1. Was ist die relative Häufigkeit von der Augenzahl 1? (!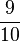) (!20%) (!
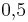) (25%) () ()
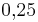Eine Münze wird 10 mal geworfen. Es fällt 7 mal Zahl. Was ist die relative Häufigkeit von Zahl? (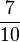
) (
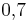) (70%) (!7%) (!
) (!)
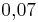Ein Reißnagel wird 30 mal geworfen, davon landet er 12 mal auf dem Kopf. Wie groß ist die dazugehörige relative Häufigkeit? () () (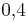40%) (!12%) (!
) (!
)
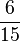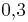Es wird 50 mal gewürfelt, 32 mal liegt eine gerade Augenzahl oben. Wie groß ist die relative Häufigkeit von der geraden Augenzahl? (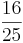
) (
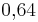) (64%) (!
) (!
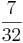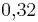) (!50%)
Eine Münze wird 100 mal geworfen, wobei 41 mal Zahl fällt. Wie groß ist die relative Häufigkeit für das Werfen von Wappen? (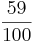
) (
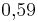) (59%) (!41%) (!) (!)
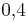Aufgabe 3:
Gewinnchancen vorhersagen mithilfe von Baumdiagrammen
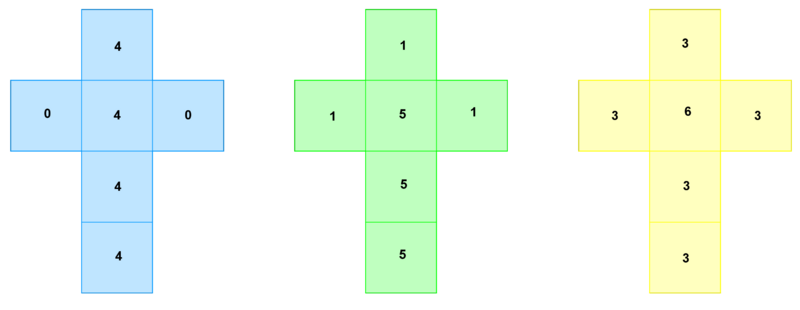
- Es sind drei Würfel gegeben, die durch die nachfolgenden Netze gezeigt werden:
- Du Spielst nun mit deinem Banknachbarn "Die höhere Augenzahl gewinnt".
Jeder würfelt einmal, der mit der höheren Augenzahl gewinnt.
- Du Spielst nun mit deinem Banknachbarn "Die höhere Augenzahl gewinnt".
- a) In folgenden Tabellen sind die Ergebnisse eures Spiels zusammengefasst.
Berechne die zugehörigen relativen Häufigkeiten und fasse dann die Ergebnisse zusammen:
- a) In folgenden Tabellen sind die Ergebnisse eures Spiels zusammengefasst.
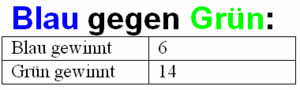
Im Spiel Blau gegen Grün:
Die relative Häufigkeit, dass Grün gewinnt, beträgt 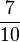und dass blau gewinnt 
.
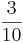Im Spiel Blau gegen Gelb:
Die relative Häufigkeit für einen Sieg für Blau ist 75% und für einen Sieg für Gelb ist die relative Häufigkeit .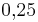
Im Spiel Grün gegen Gelb:
Die relative Häufigkeit für den Fall, dass Grün gewinnt, beträgt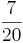 
und für den Fall, dass Gelb gewinnt beträgt die relative Häufigkeit 65%.
Als Ergebnis lässt sich daher zusammenfassen:
Grün schlägt Blau.
Blau schlägt Gelb.
Gelb schlägt Grün.
- b) Ist es besser als Erster oder als Zweiter einen Würfel auszuwählen?
Um diese Frage zu beantworten hilft dir das Wissen aus Teilaufgabe a).
- b) Ist es besser als Erster oder als Zweiter einen Würfel auszuwählen?
(!Es ist besser als Erster zu wählen) (Es ist besser als Zweiter zu wählen)
Zurück
