Prinzipielle Grenzen der Berechenbarkeit: Unterschied zwischen den Versionen
K (→Turing-Maschine) |
(→Churchsche These) |
||
| Zeile 197: | Zeile 197: | ||
== Churchsche These == | == Churchsche These == | ||
| + | |||
| + | Warum befassen wir uns mit Turing-Maschinen? | ||
| + | Das Modell der Turing-Maschinen ist die erste exakte Präzisierungen des Begriffs "Algorithmus" gewesen, d.h. | ||
| + | jede berechenbare Funktion kann durch eine Turing-Maschine realisiert werden. Umgekehrt | ||
| + | repräsentiert jede Turing-Maschine eine berechenbare Funktion. Das ist der Grund, warum sich die | ||
| + | theoretische Informatik mit Turing-Maschinen beschäftigt. | ||
| + | |||
| + | {{Merke|'''These von Church''' | ||
| + | |||
| + | Jede im intuitiven Sinne berechenbare Funktion ist auch turing-berechenbar, d.h. man kann eine Turing-Maschine entwerfen, die diese Funktion berechnet. | ||
| + | }} | ||
| + | |||
| + | Diese These kann man natürlich nicht beweisen, da der Begriff "intuitiv berechenbar" nicht mathematisch präzisiert werden kann. Man kann aber zeigen, dass die mächtigsten Berechenbarkeitsmodelle genauso mächtig sind, wie eine Turingmaschine, also auch Programmiersprachen wie Java, Pascal, Fortran, usw. | ||
== Entscheidbarkeit == | == Entscheidbarkeit == | ||
Version vom 26. September 2009, 14:42 Uhr
Inhaltsverzeichnis |
Algorithmus
Definition
Ein Algorithmus ist eine Verarbeitungsvorschrift, die aus einer endlichen Folge von eindeutig ausführbaren Anweisungen besteht, die aus endlich vielen Eingabedaten endlich viele Ausgabedaten erzeugt und mit der man eine Vielzahl gleichartiger Aufgaben lösen kann.
Wie du sicher bemerkt hast, kommt in dieser Definition sehr oft der Begriff "endlich" vor. Dies wird später noch eine entscheidende Rolle spielen!
Wobei handelt es sich um einen Algorithmus? (Lösen einer quadratischen Gleichung) (!Auflistung aller Primzahlen) (Konstruieren eines Kreises durch 3 Punkte, die nicht auf einer Gerade liegen) (Wechseln eines Autoreifens) (!Schreiben einer Eins in der Schulaufgabe)
Gödelisierung
Wir versuchen jetzt Hilfe von der Mathematik zu erhalten. Dazu wandelt man Probleme in eine Form um, die es erlaubt, Wissen über Abbildungen innerhalb der natürlichen Zahlen zu benutzen. Um dies zu erreichen, wandelt man die Ein- und Ausgabedaten in natürliche Zahlen um. Dies kann mehr oder minder geschickt erfolgen. Kurt Gödel hat sich mit solchen Fragestellungen beschäftigt, weshalb man entsprechende Verfahren Gödelisierungen nennt.
|
Die 26 Buchstaben des Alphabets werden mit den Zahlen 1 bis 26 kodiert. Damit könnte man ein geschriebenes Wort als Zahl schreiben. Dekodiere die Zahl "26235945212097"! Welche Buchstabenfolge erhält man nach dem Dekodieren?
Möglichkeiten für das dekodierte Wort sind z.B.: ZWEIDEUTIG oder BFBCEIDEBATIG oder ...
|
|
Nun werden die 26 Buchstaben des Alphabets mit den Zahlen 01 bis 26 kodiert. Schreibt man die kodierten Buchstaben hintereinander, so erhält man eine Zahl. Dekodiere die Zahl 26230509060512121519.
Das dekodierte Wort lautet: ZWEIFELLOS
|
|
Nun werden die 26 Buchstaben des Alphabets wie folgt kodiert: Den 26 Buchstaben des Alphabets wird jeweils eine eindeutige Zahl zwischen 1 und 26 zugeordnet. Ein Wort wird nun mit fortlaufenden Primzahlpotenzen kodiert, also wenn a die Zahl 1, b die Zahl 2, c die Zahl 3 zugeordnet wird, dann wird das Wort abbca wie folgt kodiert:
Multipliziert man diese Zahlen miteinander, erhält man die Zahl
Das dekodierte Wort lautet: INFORMATIK. Diese Art der Kodierung ist eher von theoretischer Bedeutung, weil man sehr schnell extrem große Zahlen erhält. Das obige Beispiel ergäbe ausmultipliziert
|
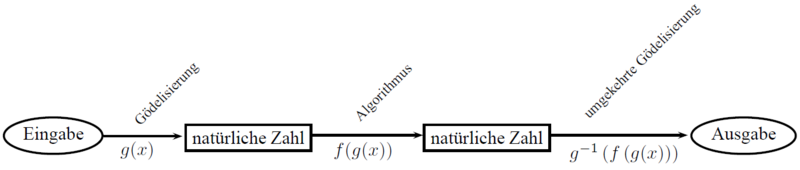
Mit der Gödelisierung lassen sich beliebige Ein- und Ausgaben in natürliche Zahlen umwandeln und umgekehrt. Diese Vorgehensweise wird häufig in der theoretischen Informatik verwendet, da sich Algorithmen dadurch als Funktionen über den natürlichen Zahlen abbilden lassen. Zur Umwandlung existieren verschiedenste Verfahren.
Definition
Eine Gödelisierung ist eine Abbildung 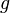 von der Menge der Ein- und Ausgaben
von der Menge der Ein- und Ausgaben 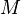 eines Algorithmus in die Menge der natürlichen Zahlen
eines Algorithmus in die Menge der natürlichen Zahlen 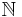 :
: 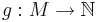 .
Die Abbildung muss dabei noch drei Bedingungen erfüllen:
.
Die Abbildung muss dabei noch drei Bedingungen erfüllen:
-
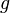 muss injektiv sein, d.h. jede natürliche Zahl darf höchstens das Bild von einem Programm sein; aber nicht jede natürliche Zahl muss auch ein Programm sein
muss injektiv sein, d.h. jede natürliche Zahl darf höchstens das Bild von einem Programm sein; aber nicht jede natürliche Zahl muss auch ein Programm sein 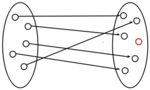
- Die Bildmenge muss entscheidbar sein, es muss also einen Algorithmus geben, der Ja ausgibt, wenn die Zahl einem Programm entspricht und Nein, wenn es sich um kein Programm handelt.
- Die Umkehrfunktion
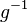 muss berechenbar sein, d.h. man muss aus der natürlichen Zahl auch wieder das Programm bekommen können.
muss berechenbar sein, d.h. man muss aus der natürlichen Zahl auch wieder das Programm bekommen können.
Welches der obigen Verfahren eignet sich für eine Gödelisierung? (!Kodierung mit Zahlen 1 bis 26) (Kodierung mit Zahlen 01 bis 26) (Kodierung mit Primzahlpotenzen)(!Keines der Verfahren)
Durch die Hilfe der Gödelisierung kann man also jeden Algorithmus als eine Abbildung von einer natürlichen Zahl auf eine andere ansehen.
Wie viele Algorithmen gibt es?
Wie bei der Definition des Begriffes Algorithmus bereits erwähnt wurde, ist der Begriff der Endlichkeit von großer Bedeutung. Da ein Algorithmus eine endliche Folge von Anweisungen ist, besteht ein Algorithmus auch nur aus endlich vielen Zeichen. Mit der oben beschriebenen Gödelisierung lässt sich also jeder Algorithmus auch als eine natürliche Zahl auffassen. Weil dann die Menge aller Algorithmen eine Teilmenge der natürlichen Zahlen ist, sind die Algorithmen abzählbar.
Durch die Gödelisierung kann man die Algorithmen als Funktionen natürlicher Zahlen ansehen. Wir schreiben die Algorithmen und die möglichen Eingaben als eine unendlich große zweidimensionale Tabelle auf. An der Seite werden die Algorithmen bzw. die Funktionen und als Spaltenüberschriften werden die möglichen Eingaben angetragen:
| 1 | 2 | 3 | 4 | 5 | ... | |
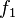 |
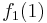 |
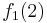 |
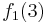 |
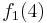 |
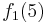 |
... |
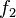 |
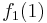 |
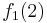 |
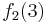 |
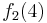 |
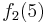 |
... |
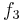 |
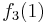 |
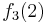 |
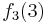 |
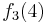 |
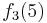 |
... |
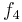 |
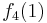 |
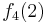 |
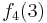 |
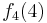 |
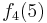 |
... |
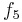 |
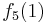 |
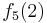 |
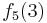 |
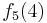 |
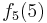 |
... |
| ... | ... | ... | ... | ... | ... | ... |
Diese Tabelle enthält alle Funktionen/Algorithmen. In der ersten Zeile stehen alle Funktionswerte der Funktion 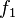 , in der zweiten Zeile stehen alle Funktionswerte der Funktion
, in der zweiten Zeile stehen alle Funktionswerte der Funktion 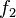 usw.
usw.
Wir definieren uns nun eine Funktion 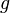 wie folgt:
wie folgt:
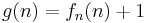
Diese Funktion ist offensichtlich berechenbar, also müsste sie irgendwo in der Folge 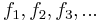 vorkommen.
Diese Funktion unterscheidet sich aber von jeder anderen Funktion in der Tabelle. Dies ist offensichtlich ein Widerspruch dazu, dass in der Tabelle alle berechenbaren Funktionen enthalten sind.
vorkommen.
Diese Funktion unterscheidet sich aber von jeder anderen Funktion in der Tabelle. Dies ist offensichtlich ein Widerspruch dazu, dass in der Tabelle alle berechenbaren Funktionen enthalten sind.
30px Merke
|
Beispiele für Probleme, die nicht algorithmisch lösbar sind:
- Fermatsche Vermutung: Es gibt keine natürlichen Zahlen
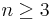 , für die positive ganze Zahlen
, für die positive ganze Zahlen 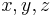 existieren mit
existieren mit 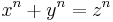 . Erst 1994 konnte Andrew Wiles diese Vermutung mit einem 100seitigen Beweis bestätigen.
. Erst 1994 konnte Andrew Wiles diese Vermutung mit einem 100seitigen Beweis bestätigen.
- Goldbachsche Vermutung: Jede gerade Zahl
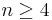 lässt sich als Summe von zwei Primzahlen darstellen. Diese Vermutung konnte bis heute weder bewiesen noch widerlegt werden.
lässt sich als Summe von zwei Primzahlen darstellen. Diese Vermutung konnte bis heute weder bewiesen noch widerlegt werden.
- Gibt es unendliche viele Primzahlzwilligen (zwei Primzahlen, die eine Differenz von 2 haben)? Diese Frage konnte bis heute nicht entschieden werden.
Turing-Maschine
Bisher haben wir uns bei der Programmierung von Algorithmen immer auf eine Programmiersprache beschränkt (Java, C, C++, C#, VisualBasic, Pascal,...). Nun stellt sich die Frage, ob die eine Programmiersprache mehr kann als die andere.
Der englische Mathematiker Alan Turing hat dazu mit seinem Modell der Turingmaschine einen entscheidenden Teil dazu beigetragen. Er entwickelte dazu ein mathematisches Modell, das das systematische Vorgehen des Menschen z.B. bei der Addition nachbildet. Man benötigt dazu einen Bleistift, ein Rechenblatt und einen Radiergummi. Auf dem Rechenblatt werden die Rechnungen sowie alle Rechenergebnisse aufgeschrieben. Mit dem Bleistift kann man Zeichen auf das Blatt schreiben und mit dem Radiergummi auch wieder löschen. Die Aktion die man ausführt hängt nur von den endlich vielen Zeichen auf dem Rechenblatt ab. Die Berechnung selbst wird durch eine Berechnungsvorschrift gesteuert.
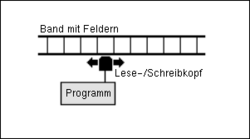
Die Turingmaschine besteht deswegen aus folgenden Komponenten:
- einem unendlich langen Speicherband mit unendlich vielen Feldern. In jedem dieser Felder ist genau ein Zeichen gespeichert. Dabei ist als Zeichen ein Blanksymbol (Leerzeichen) zugelassen, was so viel bedeutet wie „leeres Feld“. Das Blanksymbol gehört nicht zu der Menge der Eingabezeichen. Zur Vereinfachung der Vorstellung kann man auch ein endliches Band vorstellen. Dieses muss dann aber lang genug sein, damit die Berechnungen ausgeführt werden können.
- einem Schreib-/Lesekopf
- einem internen Zustand
Je nach Zustand, in dem sich die Turing-Maschine befindet, kann sie ein Zeichen auf das Band schreiben, den Schreib-/Lesekopf um ein Feld nach links oder rechts bewegen und den internen Zustand ändern.
Eine Turing-Maschine lässt sich formal folgendermaßen Beschreiben:
Definition
Eine Turingmaschine ist gegeben durch 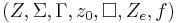 mit
mit
- einer endliche Zustandsmenge
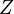
- einer endliche Menge an Eingabezeichen
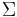
- einer Menge an zulässigen Bandzeichen
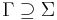
- einem Startzustand
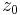
- dem Blank-Symbol

- einer Megne an Endzuständen
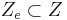
- einer Überführungsfunktion
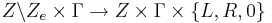 (L
(L  Schreib-/Lesekopfbewegung nach links, R
Schreib-/Lesekopfbewegung nach links, R  Schreib-/Lesekopfbewegung nach rechts, 0
Schreib-/Lesekopfbewegung nach rechts, 0  keine Schreib-/Lesekopfbewegung)
keine Schreib-/Lesekopfbewegung)
Hier findet ihr noch eine Turing-Maschinen-Simulator als Java-Anwendung (Java Runtime Environment 1.5 oder höher muss installiert sein):
(Quelle: [1]. Dort findet sich auch eine Dokumentation)
Um den Simulator zu nutzen, musst du diesen herunterladen und auf deinem Rechner entpacken. Anschließend die Datei alan-1.0.jar öffnen. Durch anklicken des Ordner-Symboles kann man vorgefertigte Turingprogramme laden und ausführen. Die Anfangskonfiguration kann man im Feld "Tape Start" angeben. Mit einem Klick auf das Play-Symbol startet die Maschine mit der Ausführung des Programms. Selbstverständlich kann man auch eigene Programme erstellen und speichern. Nähere Informationen findest du in der beigelegten PDF-Datei.
Churchsche These
Warum befassen wir uns mit Turing-Maschinen? Das Modell der Turing-Maschinen ist die erste exakte Präzisierungen des Begriffs "Algorithmus" gewesen, d.h. jede berechenbare Funktion kann durch eine Turing-Maschine realisiert werden. Umgekehrt repräsentiert jede Turing-Maschine eine berechenbare Funktion. Das ist der Grund, warum sich die theoretische Informatik mit Turing-Maschinen beschäftigt.
30px Merke
These von Church Jede im intuitiven Sinne berechenbare Funktion ist auch turing-berechenbar, d.h. man kann eine Turing-Maschine entwerfen, die diese Funktion berechnet. |
Diese These kann man natürlich nicht beweisen, da der Begriff "intuitiv berechenbar" nicht mathematisch präzisiert werden kann. Man kann aber zeigen, dass die mächtigsten Berechenbarkeitsmodelle genauso mächtig sind, wie eine Turingmaschine, also auch Programmiersprachen wie Java, Pascal, Fortran, usw.
Entscheidbarkeit
Berechenbarkeit
Fleißige Biber
Halte-Problem
|
Die Schüler der Kollegstufe besuchen |
Kontrollfragen
Warum Gödelisierung?
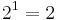 kodiert.
kodiert.
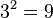 kodiert.
kodiert.
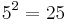 kodiert.
kodiert.
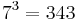 kodiert.
kodiert.
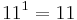 kodiert.
kodiert.
 .
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen aufsteigend ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen.
Welche Buchstabenfolge erhält man, wenn man die Zahl
.
Da die Primfaktorzerlegung eindeutig ist, wenn man die Primzahlpotenzen aufsteigend ordnet, kann man aus jeder Zahl das zugehörige Wort erzeugen.
Welche Buchstabenfolge erhält man, wenn man die Zahl 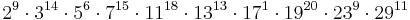 dekodiert?
dekodiert?
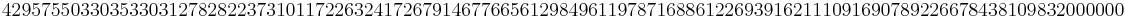 (eine 115-stellige Zahl). Es ist auch ziemlich aufwändig diese Zahlen in Primfaktoren zu zerlegen. Aus diesem Grund sind große Primzahlen für die Verschlüsselungstechnik so wichtig.
(eine 115-stellige Zahl). Es ist auch ziemlich aufwändig diese Zahlen in Primfaktoren zu zerlegen. Aus diesem Grund sind große Primzahlen für die Verschlüsselungstechnik so wichtig.
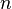 verschiedene Kurse. Jeder Kurs findet einmal pro Woche statt. Belegt ein Schüler zwei Kurse, so dürfen diese nicht gleichzeitig stattfinden. Kann man mit
verschiedene Kurse. Jeder Kurs findet einmal pro Woche statt. Belegt ein Schüler zwei Kurse, so dürfen diese nicht gleichzeitig stattfinden. Kann man mit 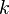 verschiedenen Terminen auskommen?
Erstelle hierzu eine Graphen, wobei ein Knoten einem Kurs entspricht. Zwei Knoten werden genau dann miteinander verbunden, wenn ein Schüler die beiden entsprechenden Kurse besucht.
Man kann die Aufgabe als sogenanntes
verschiedenen Terminen auskommen?
Erstelle hierzu eine Graphen, wobei ein Knoten einem Kurs entspricht. Zwei Knoten werden genau dann miteinander verbunden, wenn ein Schüler die beiden entsprechenden Kurse besucht.
Man kann die Aufgabe als sogenanntes 
