Würfelbau: Unterschied zwischen den Versionen
Aus DMUW-Wiki
K (Fehler) |
K (Platz und Bild) |
||
| Zeile 5: | Zeile 5: | ||
'''Mit Würfeln kannst du wieder neue Würfel bauen!''' | '''Mit Würfeln kannst du wieder neue Würfel bauen!''' | ||
<br> | <br> | ||
| − | |||
<br> | <br> | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 11: | Zeile 10: | ||
| type="{}" } | | type="{}" } | ||
{ 8 } | { 8 } | ||
| + | ||Nun löse die weiteren Aufgaben (unten)! | ||
</quiz> | </quiz> | ||
| + | <br> | ||
| + | [[Bild:So_viele_Würfel_Dorothea_Rauscher2.jpg|So_viele_Würfel|350px]] | ||
<br> | <br> | ||
*'''Um wie viel größer ist das Volumen des neuen Würfels, wenn die Kantenlänge eines kleinen Würfels 1cm beträgt?''' | *'''Um wie viel größer ist das Volumen des neuen Würfels, wenn die Kantenlänge eines kleinen Würfels 1cm beträgt?''' | ||
Version vom 10. November 2009, 17:41 Uhr
So viele Würfel
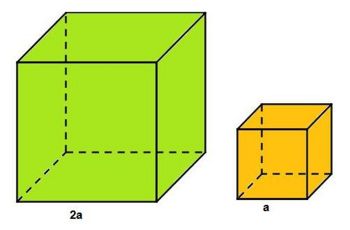
Mit Würfeln kannst du wieder neue Würfel bauen!
- Um wie viel größer ist das Volumen des neuen Würfels, wenn die Kantenlänge eines kleinen Würfels 1cm beträgt?
(Bringe die Wörter in die richtige Reihenfolge!)
Das Volumen des neuen Würfels ist achtmal so groß als das Volumen des Ausgangswürfels.
Die Oberfläche des Würfels mit doppelter Kantenlänge ist genau viermal so groß wie die Oberfläche des kleinen Würfels.
Zurück zur vorherigen Aufgabe
Weiter zur nächsten Aufgabe
