Geraden am Kreis: Unterschied zwischen den Versionen
| Zeile 114: | Zeile 114: | ||
|} | |} | ||
</div> | </div> | ||
| − | <br /><br /><br /> | + | <br /><br /><br /><br /><br /><br /><br /><br /><br /><br /> |
<br /> | <br /> | ||
'''Glückwunsch!!''' | '''Glückwunsch!!''' | ||
<br />Du hast den ersten Lernpfad erfolgreich abgeschlossen! Im nächsten Lernpfad lernst du kennen, wie sich Geraden zueinander verhalten können, aber siehe selbst! | <br />Du hast den ersten Lernpfad erfolgreich abgeschlossen! Im nächsten Lernpfad lernst du kennen, wie sich Geraden zueinander verhalten können, aber siehe selbst! | ||
| + | <br /><br /><br /><br /><br /><br /><br /> | ||
<div algin="left">[[Benutzer:David Fringes/Geraden zueinander| | <div algin="left">[[Benutzer:David Fringes/Geraden zueinander| | ||
Version vom 21. November 2009, 22:53 Uhr
 Lernpfad
|
1. Aufgabe:
Mit dieser Aufgabe sollst du mit den verschiedenen Geraden am Kreis vertraut gemacht werden.
Ordne die Begriffe und Abbildungen richtig zu. Ziehe dafür die möglichen Lösungen mit gehaltener linker Maustaste in die Felder. Anschließend kannst du dein Ergebnis überprüfen. Hast du etwas falsch zugeordnet, kannst du anschließend diese Felder neu besetzen.
 |
Zentrale |
 |
Tangente |
 |
Sekante |
 |
Passante |
3. Aufgabe:
Mit dieser Aufgabe sollen nun die Eigenschaften der Geraden am Kreis festgehalten werden.
Ziehe dafür die möglichen Lösungen mit gehaltener linker Maustaste in die Felder. Anschließend kannst du dein Ergebnis überprüfen. Hast du etwas falsch zugeordnet, kannst du anschließend diese Felder neu besetzen.
- Ist der Abstand d der Gerade g zum Kreismittelpunkt M größer als der Radius r des Kreises, so nennt man die Gerade "Passante" (Schreibweise: d(M/g) > r).
- Sind Abstand der Geraden g zum Kreismittelpunkt M und Radius r gleich groß, so nennt man die Gerade "Tangente" (Schreibweise: d(M/g) = r).
- Ist der Abstand der Gerade g zum Kreismittelpunkt M kleiner als der Radius r des Kreises, so nennt man die Gerade "Sekante" (Schreibweise: d(M/g) < r). Spezialfall: Geht die Sekante durch den Mittelpunkt M des Kreises, so nennt man sie "Zentrale".
6. Aufgabe:
Beispiel für ein richtiges Terzett: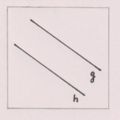 
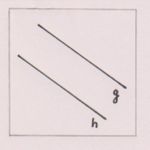
Parallele
kein Schnittpunkt
Spezialfall:
ZentraleSpezialfall:
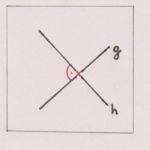
2 Schnittpunkte;
Gerade durch den Kreismittelpunkt
Tangente 1 Schnittpunkt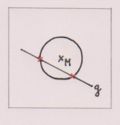 
Sekante 2 Schnittpunkte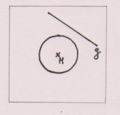 
Passante kein Schnittpunkt
7. Aufgabe:
Im Alltag kommen auch Tangenten, Sekanten und Zentralen vor.
Lass uns neue Namen erfinden!
Sekanten- 
Tangenten- 
Zentralen-
30px MerkeEine Gerade kann mit einem Kreis
- keinen Schnittpunkt gemeinsam haben. Dann nennt man sie Passante.
- einen Schnittpunkt gemeinsam haben. Dann nennt man sie Tangente (Vergleiche: Tangenten-Panzerkette).
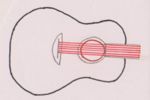
- zwei Schnittpunkte gemeinsam haben. Dann nennt man sie Sekante (Vergleiche: Sekanten-Gitarre).
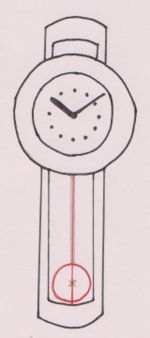
- zwei Schnittpunkte gemeinsam haben und durch den Kreismittelpunkt gehen. Dann nennt man sie Zentrale (Vergleiche: Zentralen-Pendeluhr).
Finde die verschiedenen Geraden am Kreis! (Waagrecht, senkrecht und schräg; gefundene Wörter werden grün markiert. Halte dabei die linke Maustaste gedrückt, um das Wort zu markieren)
Passante Sekante Tangente Zentrale
Glückwunsch!!
Du hast den ersten Lernpfad erfolgreich abgeschlossen! Im nächsten Lernpfad lernst du kennen, wie sich Geraden zueinander verhalten können, aber siehe selbst!
Weiter zum Lernpfad Geraden zueinander
Zurück zur Hauptseite
