Zylinder queerbeet: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 22: | Zeile 22: | ||
| <math>V=r^2\cdot \pi\cdot h_K</math> || Volumen des Zylinders | | <math>V=r^2\cdot \pi\cdot h_K</math> || Volumen des Zylinders | ||
|} | |} | ||
| − | </div> | + | </div> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
</div> | </div> | ||
<br> | <br> | ||
Version vom 25. November 2009, 10:24 Uhr
Hier werden wir nun noch einmal alles wiederholen, was wir diese Woche gelernt haben. Du benötigst hierfür dein Schulheft, Stifte, Lineal und ein Blatt Papier.
1. Aufgabe
Finde die Paare aus je einer Formel und dem dazu passenden Begriff.
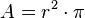 |
Flächeninhalt des Kreises |
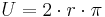 |
Umfang des Kreises |
 |
Volumen des Prismas |
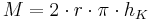 |
Mantelfläche des Zylinders |
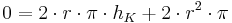 |
Oberfläche des Zylinders |
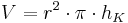 |
Volumen des Zylinders |
2. Aufgabe
Im folgenden Quiz kannst du dein Wissen zu den Lernpfaden überprüfen (manchmal gibt es auch zwei oder drei Lösungen!):
Der Durchmesser ist der (!Radius)(doppelte Radius)(!halbe Radius)
Die Oberfläche eines Zylinders besteht aus (Rechteck)(!Dreiecke)(!Raute)(Kreise)
Die Formel für das Volumen eines Zylinders lautet (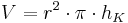 )(!
)(!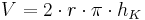 )(
)(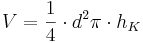 )(
)( )
)
Was stellt der Kreis in einem Zylinder dar? (!Mantelfläche) (Grundfläche) (!Oberfläche) (Deckfläche)

