Das Lot: Unterschied zwischen den Versionen
| Zeile 89: | Zeile 89: | ||
| | | | ||
|} | |} | ||
| − | + | <br /> | |
| − | + | '''Konstruktion eines Lotes mit dem Zirkel''' | |
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#8DB6CD" | ||
| + | ! Schritt 1 !! | ||
| + | |- | ||
| + | | [[Bild:Fringes_Lotkonstruktion4.jpg|450px]]|| |Hier siehst du eine Gerade g und einen Punkt P, der nicht auf der Geraden g liegt. | ||
| + | | | ||
| + | |} | ||
| + | <br> | ||
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#8DB6CD" | ||
| + | ! Schritt 2 !! | ||
| + | |- | ||
| + | | [[Bild:Fringes_Lotkonstruktion5.jpg|450px]]|| |Jetzt musst du den Zirkel in den Punkt P einstechen mit dem Radius größer als der Abstand zur Geraden g. | ||
| + | | | ||
| + | |} | ||
| + | <br> | ||
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#8DB6CD" | ||
| + | ! Schritt 3 !! | ||
| + | |- | ||
| + | | [[Bild:Fringes_Lotkonstruktion6.jpg|450px]]|| |Als nächstes erhälst du mit dem Zirkel zwei Schnittpunkte Q<sub>1</sub> und Q<sub>2</sub> mit der Geraden g. | ||
| + | | | ||
| + | |} | ||
| + | <br> | ||
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#8DB6CD" | ||
| + | ! Schritt 4 !! | ||
| + | |- | ||
| + | | [[Bild:Fringes_Lotkonstruktion7.jpg|450px]]|| |Jetzt musst du mit dem Zirkel in Q<sub>1</sub> einstechen und einen Teil eines Kreises zeichnen. Ohne den Zirkel zu verändern, stichst du nun in Q<sub>2</sub> ein und zeichnest wiederum einen Teil eines Kreises, der den ersten Teil schneiden musst. Ist dies nicht der Fall, musst du den Radius vergrößern und noch einmal neu zeichnen. | ||
| + | | | ||
| + | |} | ||
| + | <br> | ||
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#8DB6CD" | ||
| + | ! Schritt 5 !! | ||
| + | |- | ||
| + | | [[Bild:Fringes_Lotkonstruktion8.jpg|450px]]|| |Du hast den Schnittpunkt S erhalten. | ||
| + | | | ||
| + | |} | ||
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#8DB6CD" | ||
| + | ! Schritt 6 !! | ||
| + | |- | ||
| + | | [[Bild:Fringes_Lotkonstruktion9.jpg|450px]]|| |Als letztes zeichnest du eine Gerade durch den Punkt P und den Punkt S und erhälst somit das Lot zur Geraden g. | ||
| + | | | ||
| + | |} | ||
| + | <br> | ||
<br /> | <br /> | ||
Schreibe folgendes '''Merke''' in dein Heft! | Schreibe folgendes '''Merke''' in dein Heft! | ||
Version vom 28. November 2009, 00:41 Uhr
|
Lernpfad
|
1. Aufgabe:
Benutze im linken Bild mit gehaltener linker Maustaste den Schieberegler und bearbeite danach die Aufgabe rechts daneben:
| Abstand: Punkt Gerade | Aufgabe |
|---|---|
|
Benutze den Schieberegler und löse damit das Quiz! Quiz:- Auf welche Zahl α musst du den Schieberegler einstellen, damit du den kürzesten Abstand d zwischen den Punkten A und B erhältst? (α=90°) (!α=45°) (!α=77°) (!α=130°) (!α=101°) - Welche Aussage ist richtig? (Je näher die Zahl an der Zahl α=90° ist, desto kleiner ist der Abstand d zwischen den Punkten A und B) (!Je näher die Zahl an der Zahl α=90° ist, desto größer ist der Abstand d zwischen den Punkten A und B) (!Der Abstand d zwischen den Punkten A und B hat gar nichts mit dem Winkel α zu tun) - Auf welche Zahl α musst du den Schieberegler einstellen, damit du den Abstand d=2.5571 erhältst? (α=70°) (α=110°) (!α=45°) (!α=97°) (!α=106°) - Welche Aussage stimmt? (Außer bei der Zahl α=90° gibt es immer zwei Zahlen, die den gleichen Abstand d zwischen den Punkten A und B haben) (Wenn zwei Zahlen von der Zahl α=90° gleich weit entfernt sind, z.B. α=85° und α=95°, dann haben beide den gleichen Abstand d zwischen den Punkten A und B) |
2.Aufgabe
Löse das Quiz!
Achtung!! Die folgenden Aufgaben können auch mehrere richtige Antworten enthalten!
- Das Lot l schneidet die Gerade g im? (!45°-Winkel) (!60°-Winkel) (90°-Winkel) (!180°-Winkel)
- Das Lot l und die Gerade g sind zueinander? (senkrecht) (orthogonal) (!waagrecht) (!horizontal)
- Man schreibt? (!g ∥ l) (g ⊥ l)
- Welcher Punkt auf der Geraden g hat den kürzesten Abstand zum Punkt P? (Lotfußpunkt L) (!Punkt A) (!Punkt B)
Konstruktion eines Lotes mit dem Geodreieck
| Schritt 1 | ||
|---|---|---|
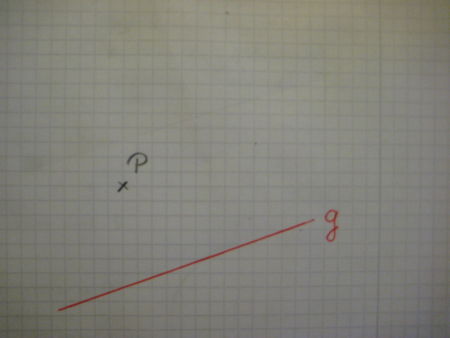 |
Hier siehst du eine Gerade g und einen Punkt P, der nicht auf der Geraden g liegt. |
| Schritt 2 | ||
|---|---|---|
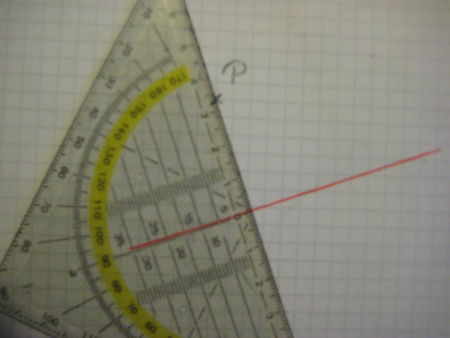 |
Jetzt musst du das Geodreieck so anlegen, dass die Zeichenkante des Geodreiecks durch den Punkt P geht und die Mittellinie des Geodreiecks auf der Geraden g liegt. |
| Schritt 3 | ||
|---|---|---|
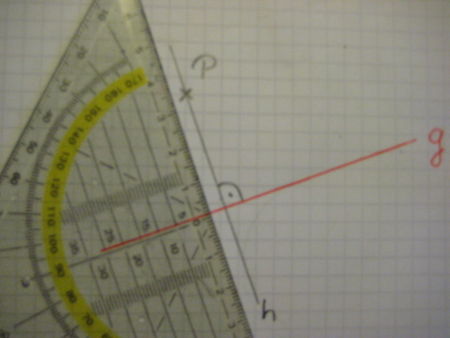 |
Als letztes ziehst du eine Linie durch den Punkt P und erhälst somit ein Lot zur Geraden g. |
Konstruktion eines Lotes mit dem Zirkel
| Schritt 1 | ||
|---|---|---|
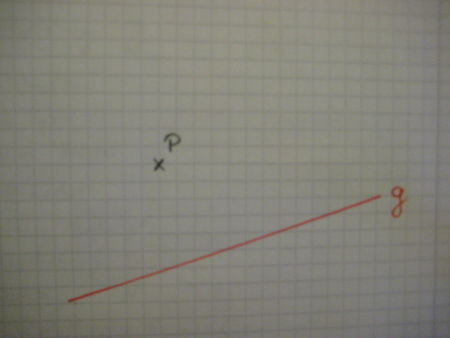 |
Hier siehst du eine Gerade g und einen Punkt P, der nicht auf der Geraden g liegt. |
| Schritt 2 | ||
|---|---|---|
 |
Jetzt musst du den Zirkel in den Punkt P einstechen mit dem Radius größer als der Abstand zur Geraden g. |
| Schritt 3 | ||
|---|---|---|
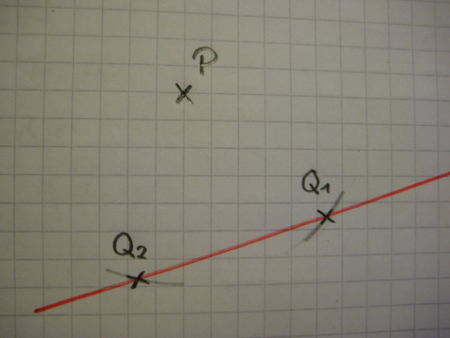 |
Als nächstes erhälst du mit dem Zirkel zwei Schnittpunkte Q1 und Q2 mit der Geraden g. |
| Schritt 5 | ||
|---|---|---|
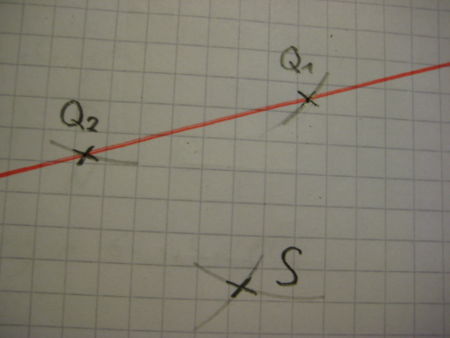 |
Du hast den Schnittpunkt S erhalten. |
| Schritt 6 | ||
|---|---|---|
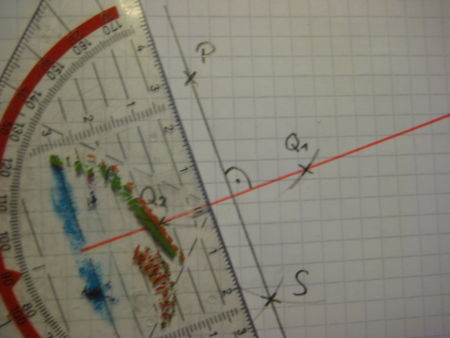 |
Als letztes zeichnest du eine Gerade durch den Punkt P und den Punkt S und erhälst somit das Lot zur Geraden g. |
Schreibe folgendes Merke in dein Heft!
30px Merke
Das Lot
|
Finde Wörter zum Thema "Lot"! (Waagrecht, senkrecht und schräg; gefundene Wörter werden grün markiert. Halte dabei die linke Maustaste gedrückt, um das Wort zu markieren)
Falls du nicht alle Wörter finden solltest, kannst du dir unter dem Quiz zuerst Tipp1 und dann Tipp2 anschauen!
| Lotfußpunkt |
| senkrecht |
| Abstand |
| orthogonal |
Spitze!
Du hast alle Lernpfade geschafft und bist jetzt ein Profi im Umgang mit Geraden,Kreis und Lot!!!

 Zurück zum Lernpfad Geraden zueinander
Zurück zum Lernpfad Geraden zueinander
