Kongruenzabbildungen/Drehung/Seite 5: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 2: | Zeile 2: | ||
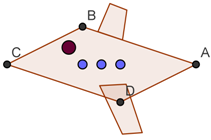
'''Schauen wir uns jetzt den Körper des Flugzeugs an.''' | '''Schauen wir uns jetzt den Körper des Flugzeugs an.''' | ||
| + | |||
| + | [[Bild:Drehung_e)MM.png|Drehung_e)MM.png]] | ||
'''Fülle dazu den Lückentext aus, indem du die verdrehten Wörter entschlüsselst!''' | '''Fülle dazu den Lückentext aus, indem du die verdrehten Wörter entschlüsselst!''' | ||
| Zeile 21: | Zeile 23: | ||
</quiz> | </quiz> | ||
| + | |||
| + | '''Entscheide jetzt, welche Aussagen auf den Körper des Flugzeugs zutreffen!'''<br/> | ||
| + | Wenn du ein bisschen nach unten scrollst, siehst du ein Applet, dass dir beim beantworten mancher Fragen helfen wird! | ||
| + | |||
<div style="border: 2px solid #FFFFFF; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid #FFFFFF; background-color:#ffffff; padding:7px;"> | ||
{|<br> | {|<br> | ||
| Zeile 26: | Zeile 32: | ||
<br> | <br> | ||
| − | |||
<quiz display="simple"> | <quiz display="simple"> | ||
Version vom 15. Dezember 2009, 21:18 Uhr
Teilaufgabe e)
Schauen wir uns jetzt den Körper des Flugzeugs an.
Fülle dazu den Lückentext aus, indem du die verdrehten Wörter entschlüsselst!
Eine Figur die durch Drehung um 180° um einen Punkt Z auf sich selbst abgebildet wird, heißt punktsymmetrisch. Der Drehpunkt wird auch Symmetriezentrum genannt. Er ist der einzige Punkt der auf sich selbst abgebildet wird und ist somit ein Fixpunkt.
Die Punktsymmetrie ist ein Sonderfall der Drehsymmetrie.
Entscheide jetzt, welche Aussagen auf den Körper des Flugzeugs zutreffen!
Wenn du ein bisschen nach unten scrollst, siehst du ein Applet, dass dir beim beantworten mancher Fragen helfen wird!
|
|