Seite 3: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 27: | Zeile 27: | ||
<br>}} | <br>}} | ||
| − | *allgemein: <math> \frac{a}{b} </math> * <math> \frac{c}{d} = | + | *'''allgemein:''' <math> \frac{a}{b} </math> * <math> \frac{c}{d} </math> = <math> \frac{a*c}{b*d} </math> |
| + | <br> | ||
| + | *'''Beispiel oben:''' <math> \frac{2}{3} </math> * <math> \frac{4}{5} </math> = <math> \frac{2*4}{3*5} </math> | ||
| + | <br> | ||
| + | *Es gilt auch das '''Kommutativgesetz!!!''' | ||
| + | |||
</div> | </div> | ||
<br> | <br> | ||
Version vom 17. Dezember 2009, 09:52 Uhr
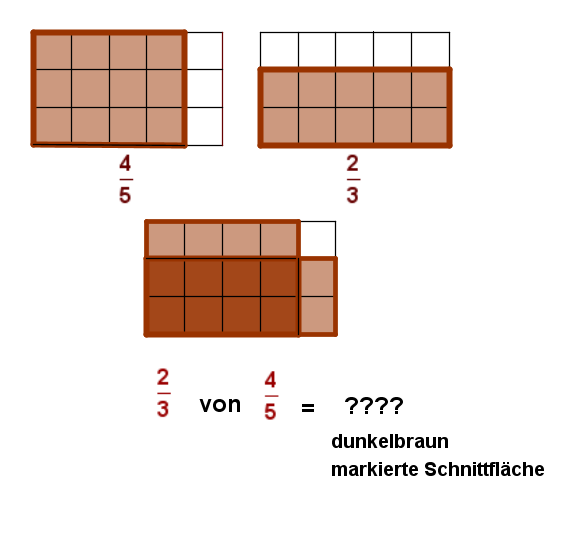
2.Station: Multiplikation zweier Brüche
Hast du nun anhand der Zeichnung die Regel der Multiplikation eines Bruches mit einer ganzen Zahl erkannt??????
Kreuze an!!! Welche Rechenregel stimmt? (!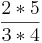 ) (
) (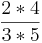 ) (
) (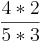 )
)
</div>
30px Merke
Multiplikation zweier Brüche
|
- allgemein:
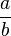 *
* 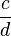 =
= 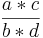
- Beispiel oben:
 *
*  =
= 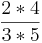
- Es gilt auch das Kommutativgesetz!!!
Die folgenden Aufgaben sollen dir zeigen, ob du die Regel verstanden hast und es anwenden kannst:
Aufgabe 1:
Berechne nun die folgenden Aufgaben und schreibe die Lösung auf deinen Laufzettel.
(kürze die Lösung soweit wie möglich und wandle in einen gemischten Bruch um)
a)*
=
b)*
=
c)*
=