Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 4: Unterschied zwischen den Versionen
| Zeile 44: | Zeile 44: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | AB ('''-3 (x-Koordinate)''' | '''2 (y-Koordinate)''') | + | AB ('''-3 (x-Koordinate)''' | '''2 (y-Koordinate)''') <br> |
</div> | </div> | ||
'''→[[Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 5|Weiter zur nächsten Teilaufgabe!]]''' | '''→[[Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 5|Weiter zur nächsten Teilaufgabe!]]''' | ||
Version vom 20. Dezember 2009, 18:44 Uhr
Teilaufgabe c)
Du hast bereits gelernt, dass die zentrische Streckung auch mit Hilfe von Vektoren durchgeführt werden kann.
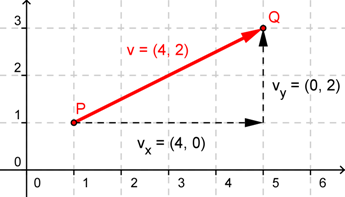
Im Applet sind jetzt die Dreiecksseiten durch Pfeile dargestellt.
1. Bearbeite zuerst den Lückentext rechts vom Applet!
|
Ziehe die richtigen Symbole und Wörter in die Lücken. Durch eine zentrische Streckung mit dem Streckungsfaktor k wird der Urpfeil PQ auf den Bildpfeil P'Q' abgebildet. Die Koordinaten des Bildpfeils erhält man durch folgende Rechnung: P'Q' = k * PQ. |
2. Gib die Koordinaten der Urpfeile an!
Weißt du nicht mehr genau, wie man Koordinaten von Pfeilen berechnet, dann lass dir folgenden Tipp anzeigen!
AB (4 (x-Koordinate) | 1 (y-Koordinate)),
BC (-2 (x-Koordinate) | 2 (y-Koordinate)),
CA (-2 (x-Koordinate) | -3 (y-Koordinate)),
3. Wie lauten die Koordinaten der Bildpfeile für k = 0,5?
Nach welcher Gleichug berechnest du die Koordinaten der Bildpfeile?
P'Q' = 2 (Zahl eintragen) * PQ
A'B' (2 (x-Koordinate) | 0,5 (y-Koordinate)),
B'C' (-1 (x-Koordinate) | 1 (y-Koordinate)),
C'A' (-1 (x-Koordinate) | -1,5 (y-Koordinate)),
4. Ein anderes Dreieck wird nun mit dem Streckungsfaktor k = -4 zentrisch gestreckt. Der Vektor AB hat nach der Streckung die Koordinaten A'B' = (12/-8). Welche Koordinaten hatte der Urpfeil AB?
AB (-3 (x-Koordinate) | 2 (y-Koordinate))