Seite 3: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 17: | Zeile 17: | ||
| + | <div style="border: 2px solid yellow; background-color:#ffffff; padding:7px;"> | ||
| + | {{Merke|'''Multiplikation zweier Brüche''' <br> | ||
| + | * Zwei Brüche werden miteinander multipliziert, indem man den '''Zähler mit Zähler''' und den '''Nenner mit dem Nenner''' '''multipliziert''' | ||
| + | * Das Ergebnis kürzt man soweit wie möglich oder wandelt es in eine gemischte Zahl um. | ||
| + | <br>}} | ||
| + | *'''allgemein:''' <math> \frac{a}{b} </math> * <math> \frac{c}{d} </math> = <math> \frac{a*c}{b*d} </math> | ||
| + | <br> | ||
| + | *'''Beispiel oben:''' <math> \frac{2}{3} </math> * <math> \frac{4}{5} </math> = <math> \frac{2*4}{3*5} </math> | ||
| + | <br> | ||
| + | *Es gilt auch das '''Kommutativgesetz!!!''' | ||
Version vom 20. Dezember 2009, 20:04 Uhr
2.Station: Multiplikation zweier Brüche
Multiplikation zweier Brüche
Beispiel:  *
* 
 *
* 
1) Multpliziere die Zähler miteinander.
2) Ebenfalls werden die Nenner beider Brüche miteinander multipliziert beiden  *
* =
= 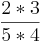
3) Kürze das Ergebnis soweit wie möglich! 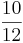 =
= 
4) Wandle den Bruch (wenn möglich) in einen gemischten Bruchum.  
30px Merke
Multiplikation zweier Brüche
|
- allgemein:
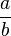 *
* 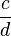 =
= 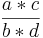
- Beispiel oben:
 *
*  =
= 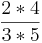
- Es gilt auch das Kommutativgesetz!!!

