Übungsaufgaben zum Satz des Thales: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
Zeile 3: Zeile 3:
 
===Übungsaufgaben zum Satz des Thales===
 
===Übungsaufgaben zum Satz des Thales===
 
}}
 
}}
 +
<br>
 +
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;">
 +
'''Hier siehst du einen schönen Regenbogen mitten in einer Berglandschaft auf dem Planet Phantasia.'''
 +
[[Bild: regenbogen_nico.jpg|thumb|left|Berglandschaft mit Regenbogen|600px]]
 +
<br>
 +
<br>
 +
<br>
 +
'''''Welcher Gipfel dieser Berglandschaft ist am spitzesten?'''''
 +
<br>
 +
<br>
 +
Frage  a): Hast du eine Idee, wie groß der Winkel am Gipfel von Berg A sein könnte?
 +
<br>
 +
<br>
 +
Antwort a): Der Berg A hat am Gipfel ein Winkelmaß von: <u style="color:lightgrey;background:lightgrey"> 90° </u>
 +
<br>
 +
<br>
 +
Frage  b): Haben die Winkel der Berge A,B,C,D, die den Regenbogen berühren eine Gemeinsamkeit?
 +
<br>
 +
<br>
 +
Antwort b): Alle Winkel, die den Regenbogen berühren sind <u style="color:lightgrey;background:lightgrey"> gleich </u> groß.
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
</div>
 +
<br>
 +
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;">
 +
'''Ein Matrose und sein Kapitän segeln zusammen am Meeresufer entlang und entdecken zwei Leuchttürme unter einem Winkel von 90°.'''
 +
[[Bild: seemann_nico.jpg|thumb|left|Leuchttürme mt Segelschiff|800px]]
 +
<br>
 +
:'''Überlegungen:'''
 +
<br>
 +
*'''Welche Position könnte denn das Segelschiff haben?'''
 +
<br>
 +
*'''Stehen die beiden Leuchttürme zueinander in Beziehung?'''
 +
<br>
 +
*'''Könnte es sich um eine geometrische Figur handeln, wenn man Objekte miteinander verbindet?
 +
<br>
 +
*'''Was bedeutet die Angabe:'''  ''"unter einem Winkel von 90°"''  '''Was kannst du daraus schließen?'''
 +
<br>
 +
<br>
 +
<div style="padding:10px;background:#ffffff;border:1px ;">
 +
'''Auf gehts - löse den Lückentext:'''
 +
<div class="lueckentext-quiz">
 +
Zwei Standorte auf dem Festland werden mit A und B bezeichnet. In der Zeichnung sind das die <strong> Leuchttürme </strong>. <br>
 +
Das Objekt im Meer, also das <strong> Segelschiff </strong> wird mit dem Buchstaben C versehen.
 +
Nun verbinden wir die Punkte A,B und C miteinander und erhalten ein <strong> rechtwinkliges Dreieck</strong>. <br>
 +
Der Winkel an der <strong> Spitze C </strong> beträgt 90°. <br>
 +
Der Matrose und sein Kapitän segeln mit dem Schiff vom linken zum rechten Leuchtturm genau so, dass der Winkel bei C stets ein Maß von 90° hat. <br>
 +
Dies lässt vermuten, dass die gefahrene Route einen <strong> Halbkreis </strong> ergibt. <br>
 +
Den Mittelpunkt dieses Halbkreises bildet die <strong> Strecke AB </strong>. <br>
 +
</div>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
<br>
 +
</div>
 +
</div>
 +
<br>
 +
<br>
 +
<div style="border: 2px solid green; background-color:#ffffff; padding:7px;">
 +
'''Anhand dieser Zeichnung kannst du den Zusammenhang erkennen, den du im Lückentext erarbeiten solltest.'''
 +
[[Bild: seemann_nico1.jpg|thumb|left|Leuchttürme mit Segelschiff "Thales"|300px]]
 +
<br>
 +
<br>
 +
Frage  a): Wenn das Schiff zum Leuchtturm B fährt, unter welchem Winkel blicken der Matrose und der Kapitän aufs Festland?
 +
<br>
 +
<br>
 +
Antwort a): Die beiden Seeleute betrachten es von einem <u style="color:lightgrey;background:lightgrey"> 90° </u> Winkel aus.
 +
<br>
 +
<br>
 +
Frage  b): Wenn aber das Schiff zum Leuchtturm A fährt, unter welchem Winkel blicken dann die Schiffsleute aufs Festland ?
 +
<br>
 +
<br>
 +
Antwort b): Dann betrachten es die Seemänner von einem <u style="color:lightgrey;background:lightgrey"> 90° </u> Winkel aus.
 +
<br>
 +
<br>
 +
{|
 +
| <div class="schuettel-quiz"> <br>
 +
Daraus können wir schließen, dass der Winkel bei C immer '''rechtwinklig''' ist,  <br>
 +
wenn die Strecke von Leuchtturm A zu Leuchtturm B der '''Durchmesser''' des '''Halbkreises''' über der Strecke AB ist.
 +
<br>
 +
<br>
 +
|</div>
 +
|}
 +
<br>
 +
<br>
 +
</div>
 +
<br>
 
<br>
 
<br>
 
<br>
 
<br>

Version vom 17. Juni 2009, 13:15 Uhr


Mathematik-digital Pfeil-3d.png
Lernpfad

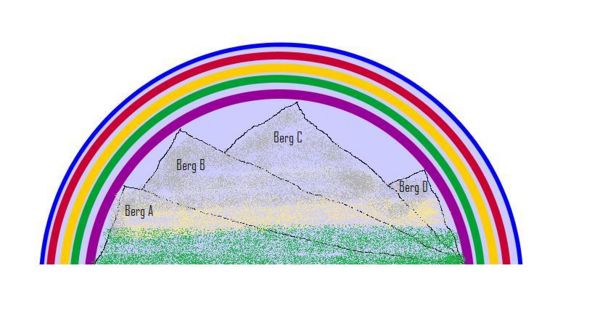
Übungsaufgaben zum Satz des Thales


Hier siehst du einen schönen Regenbogen mitten in einer Berglandschaft auf dem Planet Phantasia.

Berglandschaft mit Regenbogen




Welcher Gipfel dieser Berglandschaft ist am spitzesten?

Frage a): Hast du eine Idee, wie groß der Winkel am Gipfel von Berg A sein könnte?

Antwort a): Der Berg A hat am Gipfel ein Winkelmaß von: 90°

Frage b): Haben die Winkel der Berge A,B,C,D, die den Regenbogen berühren eine Gemeinsamkeit?

Antwort b): Alle Winkel, die den Regenbogen berühren sind gleich groß.









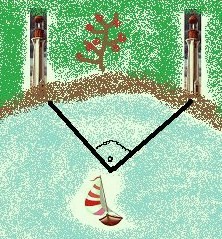
Ein Matrose und sein Kapitän segeln zusammen am Meeresufer entlang und entdecken zwei Leuchttürme unter einem Winkel von 90°.

Leuchttürme mt Segelschiff


Überlegungen:


  • Welche Position könnte denn das Segelschiff haben?


  • Stehen die beiden Leuchttürme zueinander in Beziehung?


  • Könnte es sich um eine geometrische Figur handeln, wenn man Objekte miteinander verbindet?


  • Was bedeutet die Angabe: "unter einem Winkel von 90°" Was kannst du daraus schließen?



Auf gehts - löse den Lückentext:

Zwei Standorte auf dem Festland werden mit A und B bezeichnet. In der Zeichnung sind das die Leuchttürme .
Das Objekt im Meer, also das Segelschiff wird mit dem Buchstaben C versehen. Nun verbinden wir die Punkte A,B und C miteinander und erhalten ein rechtwinkliges Dreieck.
Der Winkel an der Spitze C beträgt 90°.
Der Matrose und sein Kapitän segeln mit dem Schiff vom linken zum rechten Leuchtturm genau so, dass der Winkel bei C stets ein Maß von 90° hat.
Dies lässt vermuten, dass die gefahrene Route einen Halbkreis ergibt.
Den Mittelpunkt dieses Halbkreises bildet die Strecke AB .


















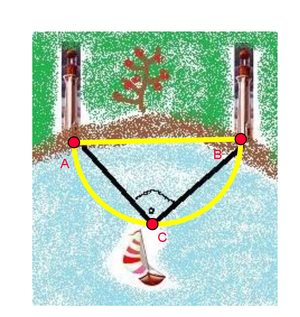
Anhand dieser Zeichnung kannst du den Zusammenhang erkennen, den du im Lückentext erarbeiten solltest.

Leuchttürme mit Segelschiff "Thales"



Frage a): Wenn das Schiff zum Leuchtturm B fährt, unter welchem Winkel blicken der Matrose und der Kapitän aufs Festland?

Antwort a): Die beiden Seeleute betrachten es von einem 90° Winkel aus.

Frage b): Wenn aber das Schiff zum Leuchtturm A fährt, unter welchem Winkel blicken dann die Schiffsleute aufs Festland ?

Antwort b): Dann betrachten es die Seemänner von einem 90° Winkel aus.


Daraus können wir schließen, dass der Winkel bei C immer rechtwinklig ist,
wenn die Strecke von Leuchtturm A zu Leuchtturm B der Durchmesser des Halbkreises über der Strecke AB ist.







Kategorie: -leicht-

  Aufgabe   Stift.gif

1. Arbeitsauftrag:




Kategorie: -mittelschwierig-

  Aufgabe   Stift.gif

2. Arbeitsauftrag:

  • Bearbeite dieses Arbeitsblatt:Kategorie mittel
  • Hier gibts die Lösungen dazu:Lösung zu Kategorie mittel




Kategorie: -schwierig-

  Aufgabe   Stift.gif

3. Arbeitsauftrag:





Die folgende Aufgabe ist zum Knüffeln für Profis gedacht!!!

Die rutschende Leiter:

Ziehe an dem grünen Punkt B Anmerkungen und Arbeitsauftrag
Was fällt dir auf, wenn du am grünen Punkt B ziehst?
Der Satz des Thales findet Anwendung beim Lösen dieses Problems.
  Aufgabe   Stift.gif

Viel Spaß beim Tüfteln:

  • Stelle dir vor, eine Leiter (hier die Strecke AB) lehnt an einer Wand.
  • Die Person, die auf der Leiter steht, befindet sich exakt in der Mitte der Strecke AB.Leiterrutschend nicoStahl.jpg
  • Frage: Hast du eine Idee auf welchem geometrischen Ort sich die Person befindet, wenn die Leiter von der Wand abrutscht?
  • Hier hast du einen Lösungsvoschlag:Die rutschende Leiter

Weitere Informationen erhaltet ihr auch auf dieser Homepage:
 Die rutschende Leiter - Universität Bayreuth








Team.gif
Entstanden unter Mitwirkung von:

Nico Stahl

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Satz_des_Thales/Übungsaufgaben_zum_Satz_des_Thales&oldid=1065“