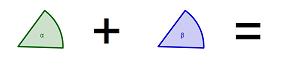Der Satz des Thales: Unterschied zwischen den Versionen

Aus DMUW-Wiki
Wechseln zu: Navigation, Suche
(→‎Ziehe am blauen Punkt C!)
Zeile 63: Zeile 63:
 
|- style="background-color:#8DB6CD"
 
|- style="background-color:#8DB6CD"
 
| <ggb_applet height="300" width="500" showResetIcon="true" filename="ThalesWERTE___nico_Nico.Stahl.ggb" /> || <ggb_applet height="300" width="500" showResetIcon="true" filename="ThalesWINKEL__Nico.Stahl.ggb" />
 
| <ggb_applet height="300" width="500" showResetIcon="true" filename="ThalesWERTE___nico_Nico.Stahl.ggb" /> || <ggb_applet height="300" width="500" showResetIcon="true" filename="ThalesWINKEL__Nico.Stahl.ggb" />
 +
|}
 +
<br>
 +
<div class="zuordnungs-quiz">
 +
<br>
 +
<big>'''Auf gehts - ordne die Bilder und Begriffe zu'''</big> <br>
 +
'''Das schaffst du  locker'''
 +
{|
 +
| Die Strecken [MA], [MB] und [MC] || sind alle gleich lang || werden mit r bezeichnet || sind der Radius des Kreises k || sind halb so lang wie der Durchmesser des Kreises k
 +
|-
 +
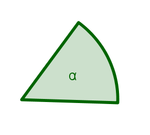
| Basiswinkel im Dreieck AMC || [[Bild:alpha_nicostahl.jpg|150px]]
 +
|-
 +
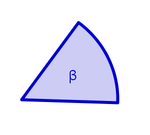
| [[Bild:beta_nicostahl.jpg|150px]] || Basiswinkel im Dreieck MBC
 +
|-
 +
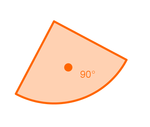
| [[Bild:alpha+beta_istgleich_nicostahl.jpg|300px]] || [[Bild:GGamma___nicostahl.jpg|150px]] || [[Bild:GGammawinkel90°__nicostahl.jpg|150px]]
 
|}
 
|}
 +
</div>
 +
<br>
 +
<br>
 
</div>
 
</div>
 
<br>
 
<br>

Version vom 17. Juni 2009, 13:39 Uhr


Mathematik-digital Pfeil-3d.png
Lernpfad

Der Satz des Thales

Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.




Betrachte aufmerksam die dynamische Animation!

 Auf gehts - Löse das Quiz!



Beziehe dich dabei auf die nebenstehende Animation.


Wenn die Strecke AB den Mittelpunkt M des Kreises schneidet, dann erscheint im Bild das Wort Thales.
Weiterhin gilt dann auch, dass der Winkel an der Spitze C (grün markiert) rechtwinklig ist.
Wenn das Dreieck ABC bei C ein Maß von 90° hat, so bezeichnet man die Strecke AB als Hypotenuse.
Die beiden Strecken AC und BC nennt man Katheten.






Betrachte aufmerksam die dynamische Animation!




Versuche den Lückentext mithilfe der dynamischen Zeichnung zu lösen.


Wenn das Dreieck ABC bei dem Eckpunkt C rechtwinklig ist, dann liegt C auf dem Halbkreis über dem Durchmesser AB.
Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das Dreieck ABC rechtwinklig bei C.

In der Mathematik kommt es häufig vor, dass Satz und Kehrsatz richtig sind.
Anstelle von zwei Sätzen in Wenn-Dann-Form, wird die Formulierung "...genau dann, wenn..." verwendet,
sowohl um die Sätze zusammenzufassen als auch um die Korrektheit der Aussage zu artikulieren.


Das Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über der Strecke AB liegt.




Ziehe am blauen Punkt C!



Auf gehts - ordne die Bilder und Begriffe zu
Das schaffst du locker

Die Strecken [MA], [MB] und [MC] sind alle gleich lang werden mit r bezeichnet sind der Radius des Kreises k sind halb so lang wie der Durchmesser des Kreises k
Basiswinkel im Dreieck AMC Alpha nicostahl.jpg
Beta nicostahl.jpg Basiswinkel im Dreieck MBC
Alpha+beta istgleich nicostahl.jpg GGamma nicostahl.jpg GGammawinkel90° nicostahl.jpg





Beweisführung für den Satz des Thales!

Klicke mit der linken Maustaste die einzelnen Schritte an.
Wenn du möchtest kannst du am Punkt C mit der Maus ziehen.



Auf gehts - löse den Lückentext:

Fülle die Lücken, indem du die passenden Begriffe zu den Feldern ziehst (mit der linken Maustaste zur Lücke ziehen und fallenlassen).


Wir wollen diesen Sachverhalt nun mathematisch untersuchen und dazu gehen wir davon aus,
dass das in der Zeichnung ersichtliche Dreieck einen rechten Winkel bei C aufzeigt.
Also sind die Punkte A, B und C gleich weit von M entfernt,
liegen somit auf dem Kreis um M,
der zugleich Mittelpunkt von der Strecke AB ist.
Das heißt, wenn das Dreieck ABC bei der Ecke C rechtwinklig ist,
dann liegt C auf dem Halbkreis über der Strecke AB.
Die Strecke AB ist zudem auch der Durchmesser des THALES-KREISES .






















Hier lernst du den Widerspruchsbeweis kennen!

Ziehe an dem roten Punkt mit der linken Maustaste. Was fällt dir auf, wenn du das Kästchen "Punkt fixieren" anklickst?









Viel Spaß beim Multiple-Choice!


Lies die folgenden Sätze konzentriert durch und klicke die korrekten Aussagen mit der linken Maustaste an. Achte auf die Fragestellungen!!!

1. Welche dieser Aussagen über das Dreieck ABC ist wahr?

Die Summe aus den Winkeln α + β ergeben zusammen immer 60°.
Die Summe der beiden Winkel α + β ist immer gleich.
Das Maß des Winkels γ an der Spitze C berechnet sich aus der Summe der Winkel α + β.
Der Winkel β kann nie doppelt so groß sein wie der Winkel α.
Der Winkel α misst immer 90°.
Der Winkel β misst immer 90°.
Der Winkel γ misst immer 90°.
Der Winkel γ misst nie 90°.
Falls gilt: α = 45°, so folgt: α = β.
Die beiden Winkel α und β sind nie maßgleich.

2. Welche dieser Aussagen über das Dreieck ABC ist falsch?

Der Winkel γ misst stets 90°.
Die zwei Winkel α und β haben niemals die gleiche Größe.
Addiert man die beiden Winkeln α + β zusammen, so erhält man stets 60°.
Das Maß des Winkels γ an der Spitze C berechnet sich aus der Summe der Winkel α + β.
Der Winkel β kann nie doppelt so groß sein wie der Winkel α.
Der Winkel α misst immer 90°.
Die Summe der beiden Winkel α + β ist immer gleich.
Der Winkel γ misst nie 90°.
Falls gilt: α = 45°, so folgt: α = β.
α kann nie das Maß 45° haben.
Der Winkel β misst immer 90°.

Punkte: 0 / 0





Nuvola apps kig.png   Merke

Der Satz des Thales:

Jedes Dreieck ∆ABC, dessen Grundseite AB dem Durchmesser eines Halbkreises entspricht und dessen Ecke C auf dem Kreisbogen liegt,
ist rechtwinklig. Den Halbkreis mit dem eingeschlossenen Dreieck bezeichnet man kurz als „Thales-Kreis“.





Hier findest du Wörter, die du beim Bearbeiten des Lernpfades kennengelernt hast.

Waagrecht und senkrecht, gefundene Wörter werden grün markiert.
Hypotenuse
Dreieck
rechtwinklig
Thalessatz
Durchmesser
Radius
Kathete
Basiswinkel
gleichschenklig
Innenwinkelsumme
Seitenhalbierende
Kongruenz
Halbkreis
Kreis
Basisseite
spitzwinklig
stumpfwinklig










































  Aufgabe   Stift.gif

Arbeitsauftrag:

  • Konstruiere in dein Übungsheft einen Thales-Kreis.
  • Schreibe die besonderen Eigenschaften eines Thales-Kreis in dein Heft.
  • Füge sonstige Besonderheiten hinzu, die dir während des Bearbeitens des Lernpfades aufgefallen sind.
  • Diskutiere in deiner Klassengemeinschaft über diesen Lernpfad



Team.gif
Entstanden unter Mitwirkung von:

Nico Stahl

Von „http://dmuw.zum.de/index.php?title=Lernpfade/Satz_des_Thales/Der_Satz_des_Thales&oldid=1068“