Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 5: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
<br> | <br> | ||
<br> | <br> | ||
| − | '''Wir wollen | + | '''Wir wollen herausfinden, in welchem Verhältnis der Punkt T die Dreiecksseite <span style="text-decoration: overline;">AB</span> teilt!'''<br/> |
| − | Berechnen wir dazu zuerst den Wert für k | + | Berechnen wir dazu zuerst den Wert für k.<br/> |
| − | + | Wenn du die Strecken wie in der letzten Teilaufgabe wieder durch Pfeile darstellst (du kannst sie dir im Applet anzeigen lassen), dann gilt:<br/> | |
| − | + | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
'''<math>\overrightarrow { AB }</math>''' = k <math>\cdot</math> '''<math>\overrightarrow { AT }</math>''' | '''<math>\overrightarrow { AB }</math>''' = k <math>\cdot</math> '''<math>\overrightarrow { AT }</math>''' | ||
</div> | </div> | ||
| − | + | Durch Einsetzen der Werte erhält man dann: | |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 41: | Zeile 40: | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| − | {Was gilt also für <span style="text-decoration: overline;">AT</span> und <span style="text-decoration: overline;">TB</span>?} | + | {Was gilt also für die Längen der Strecken <span style="text-decoration: overline;">AT</span> und <span style="text-decoration: overline;">TB</span>?} |
- <span style="text-decoration: overline;">AT</span> ist doppelt so lang wie <span style="text-decoration: overline;">TB</span> | - <span style="text-decoration: overline;">AT</span> ist doppelt so lang wie <span style="text-decoration: overline;">TB</span> | ||
| Zeile 55: | Zeile 54: | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| − | Der Punkt T teilt die Dreieckssseite AB also im Verhältnis '''1:1'''. T ist der '''Mittelpunkt''' der Dreiecksseite <span style="text-decoration: overline;">AB</span>. Die Punkte | + | Der Punkt T teilt die Dreieckssseite AB also im Verhältnis '''1:1'''. T ist der '''Mittelpunkt''' der Dreiecksseite <span style="text-decoration: overline;">AB</span>. Die Punkte U und V teilen die anderen beiden Dreiecksseiten im selben Verhältnis. Die Punkte T, U und V werden deshalb auch '''Seitenmittelpunkte''' des Dreiecks ABC genannt.<br/> |
| − | Verbindet man die Seitenmittelpunkte mit den gegenüberliegenden '''Eckpunkten''', | + | Verbindet man die Seitenmittelpunkte mit den gegenüberliegenden '''Eckpunkten''' (klicke das entsprechende Kästchen im Applet an), dann erhält man die '''Seitenhalbierenden''' des Dreiecks. Diese schneiden sich alle in einem Punkt. Im Applet ist dieser Punkt die '''Nase des Gesichts'''. Er wird '''Schwerpunkt''' des Dreiecks genannt und teilt jede Seitenhalbierende im Verhältnis '''2:1'''. |
</div> | </div> | ||
'''→[[Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 6|Auf geht's zur letzten Teilaufgabe!]]''' | '''→[[Ähnlichkeitsabbildung/Zentrische Streckung mit Hilfe von Vektoren/Seite 6|Auf geht's zur letzten Teilaufgabe!]]''' | ||
Version vom 27. Dezember 2009, 10:46 Uhr
Teilaufgabe d)
In dieser Teilaufgabe beschäftigen wir uns nur noch mit der Urfigur!
Wir wollen herausfinden, in welchem Verhältnis der Punkt T die Dreiecksseite AB teilt!
Berechnen wir dazu zuerst den Wert für k.
Wenn du die Strecken wie in der letzten Teilaufgabe wieder durch Pfeile darstellst (du kannst sie dir im Applet anzeigen lassen), dann gilt:
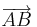 = k
= k 
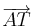
Durch Einsetzen der Werte erhält man dann:
 |
|
|
= k  |
|
|
 k = 2 (Zahl eintragen)
k = 2 (Zahl eintragen)
Ordne jetzt die passenden Begriffe den Lücken zu!
Der Punkt T teilt die Dreieckssseite AB also im Verhältnis 1:1. T ist der Mittelpunkt der Dreiecksseite AB. Die Punkte U und V teilen die anderen beiden Dreiecksseiten im selben Verhältnis. Die Punkte T, U und V werden deshalb auch Seitenmittelpunkte des Dreiecks ABC genannt.
Verbindet man die Seitenmittelpunkte mit den gegenüberliegenden Eckpunkten (klicke das entsprechende Kästchen im Applet an), dann erhält man die Seitenhalbierenden des Dreiecks. Diese schneiden sich alle in einem Punkt. Im Applet ist dieser Punkt die Nase des Gesichts. Er wird Schwerpunkt des Dreiecks genannt und teilt jede Seitenhalbierende im Verhältnis 2:1.

