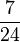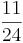Version vom 29. Dezember 2009, 11:54 Uhr

Lernpfad

Addition von Brüchen

In diesem Lernpfad wird die Addition von Brüchen mit jeweils einer kurzen Einführung und Übungsaufgaben wiederholt.

Addition von gleichnahmigen Brüchen
Addition von ungleichnahmigen Brüchen mit Nenner als Vielfache

Zeitbedarf: 35 Min.
Material: Laufzettel und einen Stift

1.Station: Addition von gleichnahmigen Brüchen

Einführung:
Svenja geht jeden Morgen um 7.00 Uhr aus dem Haus, um pünklich in der Schule zu sein. Sie muss 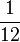$\frac{1}{12}$ h zu Fuß zur Bushaltestelle laufen. Dort steigt sie in den Schulbus ein, der 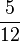$\frac{5}{12}$ h bis zur Schule braucht.

Wie lange ist sie insgesamt unterwegs?

Die Veranschaulichung durch den Schieberegler hilft dir beim Lösen der Aufgabe. Indem du den Schieberegler mit der linken Maustaste nach rechts verschiebst, ändert sich der jeweilige Zähler. Der Nenner bleibt stets gleich.

Nun ist es deine Aufgabe, die Zeit, die Svenja unterwegs ist mit dem Schieberegler zu berechnen. Gebe dazu in dem ersten Schieberegler die 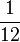$\frac{1}{12}$ h ein und addiere die 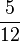$\frac{5}{12}$ h im zweiten Schieberegler. Gelingt dir dies, kannst du auf der rechten Seite das Ergebnis in den dargestellten Uhren ablesen.

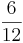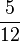Welche Lösungen sind richtig? ( $\frac{6}{12}$ ) (! $\frac{5}{12}$ ) ( $\frac{1}{2}$ )

Berechne nun die folgenden Aufgaben mit Hilfe des Schiebereglers und schreibe die Lösung auf deinen Laufzettel.

(kürze die Lösung soweit wie möglich)

a)  +  
b)  +  
c)  +

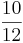
Damit du sicher gehen kannst, dass du die Addition von gleichnahmigen Brüchen verstanden hast, versuche in dem Memory verschiedenen Aufgabenstellungen das richtige Ergebnis (als Bild und als Bruch) zuzuordnen.

Memory

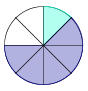
	$\frac{1}{8}$ + $\frac{5}{8}$	$\frac{3}{4}$
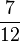
	$\frac{4}{12}$ + $\frac{3}{12}$	$\frac{7}{12}$
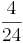	$\frac{4}{24}$ + $\frac{7}{24}$	$\frac{11}{24}$
	$\frac{1}{8}$ + $\frac{2}{8}$	$\frac{3}{8}$

→Hier geht's zur 2. Seite

@@ Zeile 66: / Zeile 66: @@
-An den Beispielen sind dir bestimmt Rechenregeln aufgefallen wie Brüche addiert werden.
-Die wichtigsten Regeln, an die du denken musst, sind hier nun aufgelistet:
-<div style="border: 2px solid red; background-color:#ffffff; padding:7px;">
-{{Merke|'''Addition gleichnahmiger Brüche''' <br>
-* Gleichnahmige Brüche werden addiert, indem man die '''Zähler addiert''' und der '''gemeinsame Nenner beibehalten''' wird.
-* Das Ergebnis kürzt man soweit wie möglich oder wandelt es in eine gemischte Zahl um.
-}}
-</div>
-<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
-Beispiel "Uhr" von oben:  <math> \frac{1}{12} </math>h + <math> \frac{5}{12} </math> = <math> \frac{1 + 5}{12} </math>h = <math> \frac{6}{12} </math>h = <math> \frac{1}{2} </math>h &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
-[[Bild:Ann-Kathrin_Hey_Uhr.png]]
-</div>

Lernpfad1: Unterschied zwischen den Versionen

Version vom 29. Dezember 2009, 11:54 Uhr

1.Station: Addition von gleichnahmigen Brüchen

Navigationsmenü

Meine Werkzeuge

Namensräume

Varianten

Ansichten

Aktionen

Suche

Navigation

Werkzeuge