Aufgaben 8. Klasse/Kongruenz/Seite 5: Unterschied zwischen den Versionen
| Zeile 62: | Zeile 62: | ||
<span style="color:#CD2626">Tipp</span> {{Versteckt| | <span style="color:#CD2626">Tipp</span> {{Versteckt| | ||
[[Erinnere dich nochmal,wie du die Strecke in Teilaufgabe a) ausgerechnet hast! Du brauchst die Gleichung nur umstellen! Die Geschwindigkeit ist im Applet angegeben!]]}} | [[Erinnere dich nochmal,wie du die Strecke in Teilaufgabe a) ausgerechnet hast! Du brauchst die Gleichung nur umstellen! Die Geschwindigkeit ist im Applet angegeben!]]}} | ||
| + | |||
| + | <popup name="Formel"> | ||
| + | <big><math>\mathit{Geschwindigkeit}</math></big> = <math>\frac{Strecke}{Zeit}</math> | ||
| + | </popup> | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Version vom 3. Januar 2010, 11:52 Uhr
Teilaufgabe f)
Jetzt ist deine Kenntnis der Mathematik gefragt! Erinnere dich an den Stoff der 6. Klasse
Ermittle die kürzeste Entfernung, die das Schiff vom Leuchtturm hatte
| Zeichnung | Aufgabe |
|---|---|
|
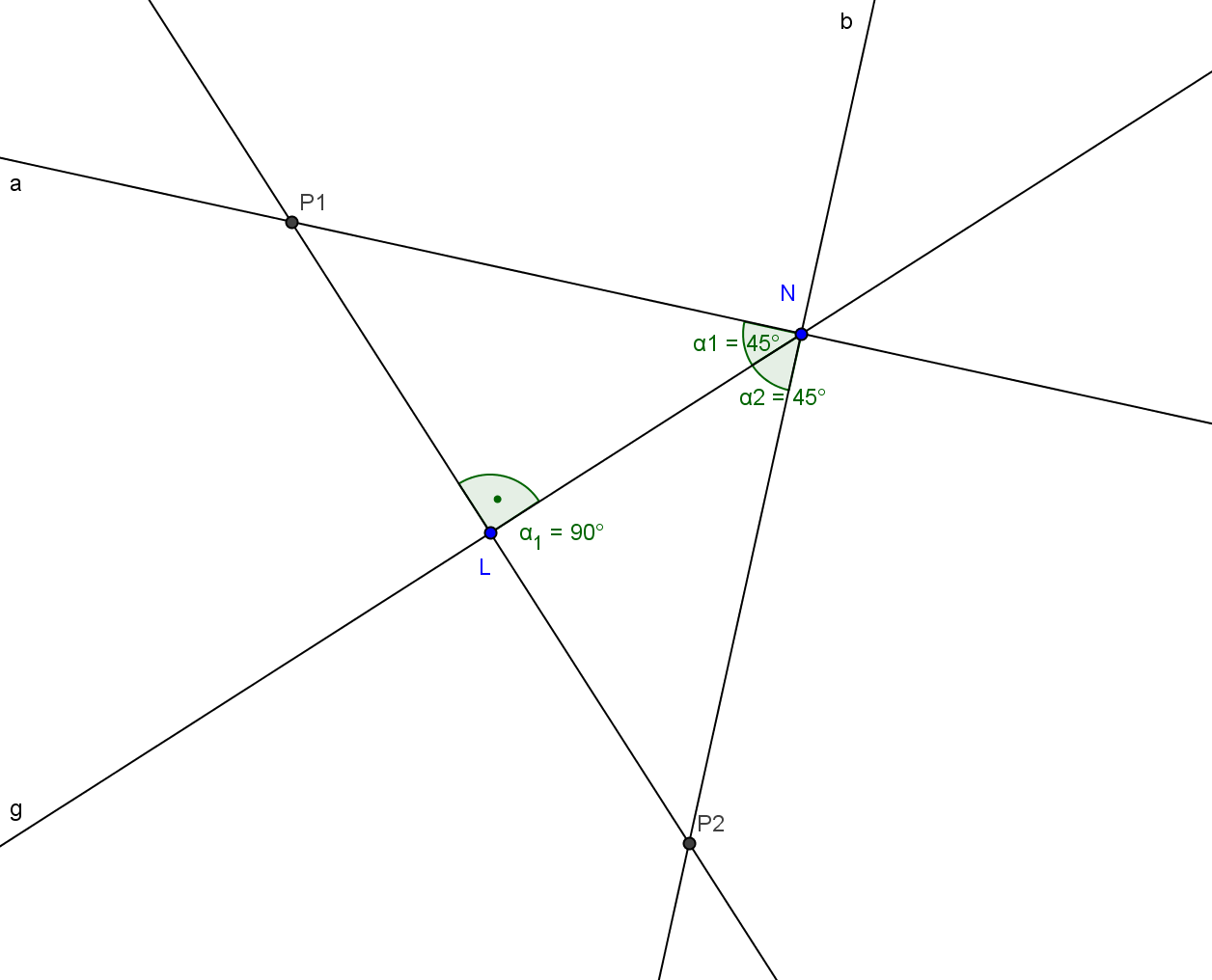
Schau dir zur Erinnerung folgende Zeichnung an! Was erkennst du? Fülle damit den kurzen Lückentext darunter aus
Die kürzeste Entfernung eines Punktes zu einer Geraden nennt man das Lot(Name) durch diesen Punkt auf die Gerade. Ein Lot steht immer senkrecht(Eigenschaft des Winkels) auf einer Geraden. |
1. Du kennst nun wieder die Eigenschaften eines Lotes. Gib jetzt die kürzeste Entfernung l des Schiffes in Metern von dem Leuchtturm an, indem du den Punkt Schiff im Applet verschiebst!
Du kannst dir die "Entfernung" des Schiffs zum Punkt C anzeigen lassen!
l = 3,42(m)
Das Schiff liegt somit auf dem Lot-Fußpunkt von C auf der Geraden AB.
2. Gib die Koordinaten an, wo das Schiff in der Zeichnung sein müsste.
Schiff = (2(x- Koordinate)/-2(y- Koordinate))
3. Bis dahin ist das Schiff 4 km gefahren!
Wie lang hat es dafür gebraucht?
Runde auf ganze Zahlen!!
Tipp
Das Schiff braucht 9(Minuten) bis zum Lotfußpunkt!
→Super gemacht! Das war viel! Jetzt darfst du noch ein Kreuzworträtsel lösen!
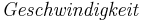 =
=