Seite 3: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
[[Bild:Sandra_Hemrich_enaktiv3.png|600px]] = '''3 (Zähler)''' /'''4 (Nenner)''' | [[Bild:Sandra_Hemrich_enaktiv3.png|600px]] = '''3 (Zähler)''' /'''4 (Nenner)''' | ||
</div> | </div> | ||
| − | |||
</div> | </div> | ||
| + | | ||
</div> | </div> | ||
| + | |||
<div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid red; background-color:#ffffff; padding:7px;"> | ||
Version vom 4. Januar 2010, 12:45 Uhr
2.Station: Multiplikation zweier Brüche

Versuche die Aufgaben zu lösen und klicke danach auf "Prüfen". Die richtige Lösung wird mit grün angezeigt. Falsche Lösungen sind rot!!!
Multiplikation zweier Brüche
 *
* 
1) Multpliziere die Zähler miteinander.
2) Ebenfalls werden die Nenner beider Brüche miteinander multipliziert beiden  *
* =
= 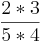
3) Kürze das Ergebnis soweit wie möglich! 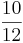 =
= 
4) Wandle den Bruch (wenn möglich) in einen gemischten Bruchum.  
 
Überprüfe, ob du die Multiplikation zweier Brüche verstanden hast
 *
*  = (
= (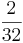 ) (
) (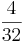 ) (!
) (! )
)
 *
*  = (
= (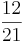 ) (
) ( ) (!
) (!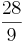 )
)
 *
*  = (!
= (! ) (!
) (!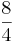 ) (!
) (!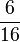 )
)



 *
* 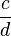 =
= 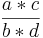
 *
*  =
=