Kongruenzabbildungen/Parallelverschiebung/Seite 4: Unterschied zwischen den Versionen
| Zeile 11: | Zeile 11: | ||
</div> | </div> | ||
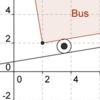
| − | ''' | + | '''Bevor du berechnen kannst wie steil der Berg ist, auf dem der Bus fährt, musst du das Puzzle zusammenfügen. Rechts siehst du das fertige Bild.''' |
| − | + | ||
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
Version vom 6. Januar 2010, 21:01 Uhr
Teilaufgabe e)
Jetzt noch etwas, das du bestimmt schon einmal gesehen hast.
.gif)
Der Berg an dem das Schild angebracht ist, das du links siehst, hat eine Steigung von 12%.
Das bedeutet, dass pro 100m in waagrechter Richtung die Höhe des Berges um 12m zunimmt.
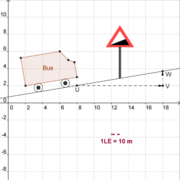
Bevor du berechnen kannst wie steil der Berg ist, auf dem der Bus fährt, musst du das Puzzle zusammenfügen. Rechts siehst du das fertige Bild.
MM.png)
MM1a.png)
|
MM2a.png)
|
MM3a.png)
|
MM4a.png)
|
MM5a.png)
|
MM6a.png)
|
MM7a.png)
|
MM8a.png)
|
MM9a.png)
|
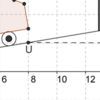
Gib zuerst die Koordinaten der Punkte U und V an.
U (8 (x-Koordinate) | 2 (y-Koordinate)),
V (18 (x-Koordinate) | 2 (y-Koordinate))
Welche Länge hat der Verbindungsvektor zwischen U und V? Gib die Länge in Meter an.
100 (m)
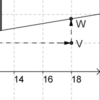
Der Punkt W hat die Koordinaten (18|3,7). Welche Länge hat somit der Verbindungsvektor zwischen V und W?
17 (m)
Welche Zahl in Prozent muss also auf dem Schild stehen?
17 (%)
