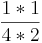Version vom 7. Januar 2010, 00:49 Uhr

2.Station: Multiplikation zweier Brüche

Einführung:

Susi hat am nächsten Tag eine Tafel Schokolade in der Schule dabei. Als sie angefangen hat zu essen, kommt Tom dazu und möchte auch etwas haben!!!
(Bild: Tom und Susi mit Sprechblasen)

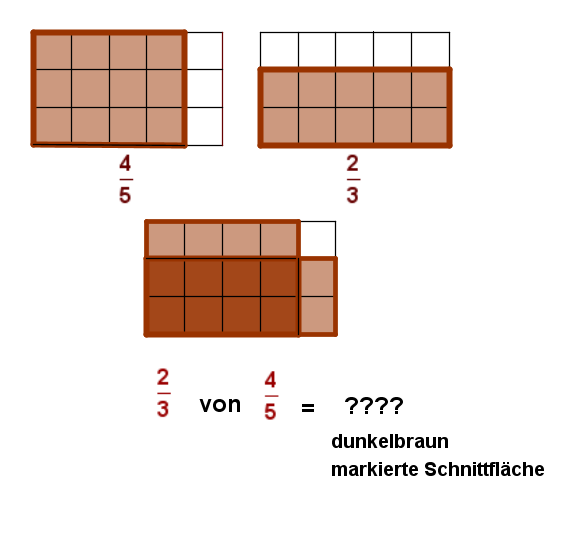
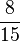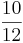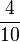Hast du nun anhand der Zeichnung erkannt welchen Bruchteil der Schokolade Tom bekommt?????? ( $\frac{8}{15}$ ) (! $\frac{10}{12}$ ) (! $\frac{4}{10}$ )

Tom, Susi und Martin spielen alle ein Instrument und können Noten lesen!!! Kannst du das auch???

Erkennst du, welchen Wert die Noten haben???
Versuche die Aufgaben zu lösen und klicke danach auf "Prüfen". Die richtige Lösung wird mit grün angezeigt. Falsche Lösungen sind rot!!!

=( $\frac{1}{32}$ )(! $\frac{2}{32}$ )

= (1 $\frac{1}{16}$ ) (! $\frac{1}{16}$ )

= ( $\frac{1}{8}$ ) (! $\frac{1}{6}$ )

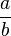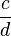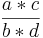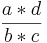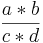Kreuze an!!! Welche Rechenregel stimmt für $\frac{a}{b}$ * $\frac{c}{d}$ ? ( $\frac{a*c}{b*d}$ ) (! $\frac{a*d}{b*c}$ ) (! $\frac{a*b}{c*d}$ )

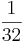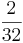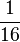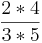
Multiplikation zweier Brüche

Zwei Brüche werden miteinander multipliziert, indem man den Zähler mit Zähler und den Nenner mit dem Nenner multipliziert
Das Ergebnis kürzt man soweit wie möglich oder wandelt es in eine gemischte Zahl um.