Kongruenzabbildungen/Drehung/Seite 2b: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 46: | Zeile 46: | ||
- [ZP] II [ZP'] | - [ZP] II [ZP'] | ||
| − | + [ZP] <math>\perp</math> [ZP'] | + | + [ZP]<math>\perp</math>[ZP'] |
+ Man erhält die Koordinaten des Bildpfeils <math>\overrightarrow { ZP' }</math> durch vertauschen der Koordinaten des Urpfeils <math>\overrightarrow { ZP }</math> | + Man erhält die Koordinaten des Bildpfeils <math>\overrightarrow { ZP' }</math> durch vertauschen der Koordinaten des Urpfeils <math>\overrightarrow { ZP }</math> | ||
Version vom 7. Januar 2010, 20:18 Uhr
Teilaufgabe c)
Schauen wir uns die Drehung um 90° noch einmal ein bisschen genauer an!
Das war doch gar nicht so schwer, oder? Üben wir das noch einmal an zwei Beispielen!
1. Gib zuerst die Koordinaten des Urpfeils 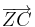 an, wenn der Punkt C(2|14) um den Punkt Z(1|1) um 90° gedreht wird!
an, wenn der Punkt C(2|14) um den Punkt Z(1|1) um 90° gedreht wird!
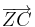 = = |
|
|
Nach dem was du gerade gelernt hast ist es jetzt ganz einfach, die Koordinaten des Pfeils 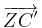 zu berechnen!
zu berechnen!
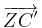 = = |
|
|
2. Das Flugzeug wird jetzt um das Zentrum Z(4|-2) um 90° gedreht. Berechne die Koordinaten des Ur- und des Bildpfeils 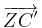 !
!
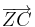 = = |
|
|
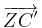 = = |
|
|
Welche Koordinaten hat der Punkt C'?
C' (-3 (x-Koordinate) | 9 (y-Koordinate))
→Du hast das toll gemacht! Auf geht's zur nächsten Teilaufgabe!
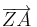 und des Bildpfeils
und des Bildpfeils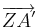 !
!
