Seite 3: Unterschied zwischen den Versionen
| Zeile 43: | Zeile 43: | ||
<div style="border: 2px solid yellow; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid yellow; background-color:#ffffff; padding:7px;"> | ||
'''Multiplikation zweier Brüche''' <br> | '''Multiplikation zweier Brüche''' <br> | ||
| + | * Zwei Brüche werden miteinander multipliziert, indem man den '''Zähler mit Zähler''' und '''Nenner mit Nenner''' '''multipliziert''' | ||
| + | * Das Ergebnis kürzt man soweit wie möglich oder wandelt es in einen gemischten Bruch um. | ||
<br> | <br> | ||
| − | + | |} | |
| − | * | + | </div> |
| + | {| | ||
| + | | '''Allgemein: || | ||
| + | <div style="border: 2px solid yellow; background-color:#ffffff; padding:7px;"> <math> \frac{a}{b} </math> * <math> \frac{c}{d} </math> = <math> \frac{a*c}{b*d} </math> | ||
| + | </div> | ||
| + | |} | ||
| + | |||
<br> | <br> | ||
| − | *''' | + | *''' Beispiel oben:''' |
| + | Anhand der Zeichnung wird die Multiplikation zweier Brüche nochmals veranschaulicht. | ||
| + | Wie du sehen kannst, ist die Multiplikationsaufgabe genau die gelb/grün schraffierte Fläche! | ||
| + | Ebenfalls erkennst du, dass das Wort '''von''' mit dem mathematischen Zeichen '''*''' übersetzt werden kann! | ||
<br> | <br> | ||
| − | + | [[Bild:Sandra_Hemrich_Bild_Einführung.jpg]] [[Bild:Sandra_Hemrich_Bild2_Einführung.jpg]] | |
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
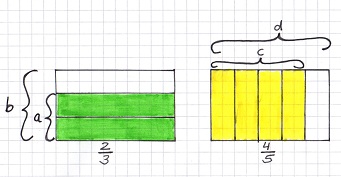
| + | <math> \frac{2}{3} </math> * <math> \frac{4}{5} </math> = <math> \frac{2*4}{3*5} </math> = '''<math> \frac{8}{15} </math> (gelb/grün schraffierte Fläche)''' | ||
| + | <br> | ||
| + | |||
| + | |||
<br> | <br> | ||
<br> | <br> | ||
Version vom 8. Januar 2010, 12:13 Uhr
2.Station: Multiplikation zweier Brüche
Einführung:
enaktiv-> Schieberegler
Überprüfe, ob du die Multiplikation zweier Brüche verstanden hast!!! Benutze dabei den Schieberegler!!!
 *
*  = (
= (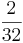 ) (
) (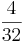 ) (!
) (! )
)
 *
*  = (
= (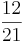 ) (
) ( ) (!
) (!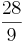 )
)
 *
*  = (!
= (! ) (!
) (!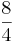 ) (!
) (!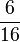 )
)
Multiplikation zweier Brüche
 *
* 
1) Multpliziere die Zähler miteinander.
2) Ebenfalls werden die Nenner beider Brüche miteinander multipliziert beiden  *
* =
= 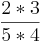
3) Kürze das Ergebnis soweit wie möglich! 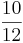 =
= 
4) Wandle den Bruch (wenn möglich) in einen gemischten Bruchum.
| Allgemein: |
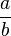 * * 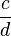 = = 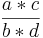
|
- Beispiel oben:
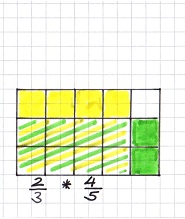
Anhand der Zeichnung wird die Multiplikation zweier Brüche nochmals veranschaulicht.
Wie du sehen kannst, ist die Multiplikationsaufgabe genau die gelb/grün schraffierte Fläche!
Ebenfalls erkennst du, dass das Wort von mit dem mathematischen Zeichen * übersetzt werden kann!
 *
*  =
= 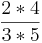 =
= 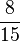 (gelb/grün schraffierte Fläche)
(gelb/grün schraffierte Fläche)


