Beweisführung des Umfangswinkelsatzes: Unterschied zwischen den Versionen
K (→Beweisführung für den Satz des Thales!) |
|||
| Zeile 14: | Zeile 14: | ||
| <ggb_applet height="500" width="650" showResetIcon="true" filename="BeweisführungdesThales_nico.ggb" /> || <div class="zuordnungs-quiz"> | | <ggb_applet height="500" width="650" showResetIcon="true" filename="BeweisführungdesThales_nico.ggb" /> || <div class="zuordnungs-quiz"> | ||
<big>'''Zuordnung'''</big><br> | <big>'''Zuordnung'''</big><br> | ||
| − | Ordne den einzelnen Schritten | + | Ordne den einzelnen Schritten den jeweils passenden Text zu. |
{| | {| | ||
| Schritt 1 || Dreieck AMC und Dreieck MBC sind gleichschenklig. (r=r) | | Schritt 1 || Dreieck AMC und Dreieck MBC sind gleichschenklig. (r=r) | ||
Version vom 23. Juni 2009, 16:54 Uhr
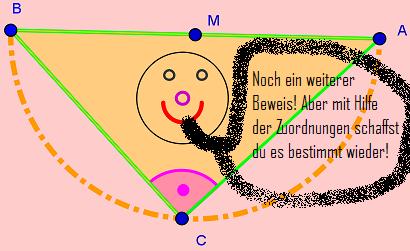
Beweisführung für den Satz des Thales!
Klicke mit der linken Maustaste die einzelnen Schritte an.
Wenn du möchtest kannst du am Punkt C mit der Maus ziehen.
|
|
Zuordnung
Basiswinkel sind maßgleich: α = α Schritt 1 α + β = γ Schritt 4 Basiswinkel sind maßgleich: β = β Schritt 2Dreieck AMC und Dreieck MBC sind gleichschenklig. (r=r)Schritt 5Innenwinkelsumme im Dreieck ABC=180°: α + α + β + β = 180°
|
- Hast du Lust auf noch eine weitere Beweisführung?
- Auf geht's - viel Spaß beim Zuordnen der Begriffe!
- Wenn du willst, dann kannst du auch am blauen Punkt C ziehen!
| Beweisführung für den Satz des Thales: | Ordne die Begriffe unten den richtigen Oberbegriffen zu!: |
|---|---|
|
|
Zuordnung
Schritt 2 Gerade g ist parallel zu Strecke [AB] Schritt 6 Schritt 3 Schritt 4 Schritt 7 Schritt 5 Wechselwinkel an parallelen Geraden sind gleich groß: α=α und β=βBasiswinkel sind gleich groß: α=α und β=βNebenwinkel ergänzen sich zu 180°:
|