Lernpfad2 Seite 3: Unterschied zwischen den Versionen
| Zeile 6: | Zeile 6: | ||
| − | =2. Addition von | + | =2. Addition von ungleichnamigen Brüchen= |
<div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
| − | '''Zum Frühstück hat Svenja schon <math> \frac{1}{4} </math> Liter Schokomilch getrunken. Nach Unterrichtsschluss hat sie auch ihre <math> \frac{1}{2} </math> Liter Flasche''' '''Apfelsaftschorle leer getrunken. | + | '''Zum Frühstück hat Svenja schon <math> \frac{1}{4} </math> Liter Schokomilch getrunken. Nach Unterrichtsschluss hat sie auch ihre <math> \frac{1}{2} </math> Liter Flasche''' '''Apfelsaftschorle leer getrunken.''' |
| − | + | ||
| − | + | ||
| − | + | ||
[[Bild:Ann-Kathrin_Hey_Messbecher_Einführung.png]] | [[Bild:Ann-Kathrin_Hey_Messbecher_Einführung.png]] | ||
| Zeile 19: | Zeile 16: | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
| − | Wie viel Liter hat Svenja geschafft, wenn sie <math> \frac{1}{4} </math> Liter Schokomilch und <math> \frac{1}{2} </math> Liter Apfelsaftschorle getrunken hat? (!<math> \frac{1}{8} </math>Liter) (<math> \frac{3}{4} </math>Liter) (!<math> \frac{2}{6} </math>Liter) | + | '''Wie viel Liter hat Svenja geschafft, wenn sie <math> \frac{1}{4} </math> Liter Schokomilch und <math> \frac{1}{2} </math> Liter Apfelsaftschorle getrunken hat?''' (!<math> \frac{1}{8} </math>Liter) (<math> \frac{3}{4} </math>Liter) (!<math> \frac{2}{6} </math>Liter) |
| Zeile 85: | Zeile 82: | ||
'''Damit du immer weisst, wie du bei der Addition ungleichnamiger Brüche vorgehen musst, fülle den Lückentext mit den richtigen Wörtern aus!''' | '''Damit du immer weisst, wie du bei der Addition ungleichnamiger Brüche vorgehen musst, fülle den Lückentext mit den richtigen Wörtern aus!''' | ||
| − | Das Beispiel | + | Das Beispiel soll dir eine kleine Hilfe sein. |
{| | {| | ||
|[[Bild:Ann-Kathrin_Hey_Animation_Ausrufezeichen.png]]|| | |[[Bild:Ann-Kathrin_Hey_Animation_Ausrufezeichen.png]]|| | ||
Version vom 10. Januar 2010, 10:32 Uhr

|
2. Addition von ungleichnamigen Brüchen
Zum Frühstück hat Svenja schon  Liter Schokomilch getrunken. Nach Unterrichtsschluss hat sie auch ihre
Liter Schokomilch getrunken. Nach Unterrichtsschluss hat sie auch ihre  Liter Flasche Apfelsaftschorle leer getrunken.
Liter Flasche Apfelsaftschorle leer getrunken.
Wie viel Liter hat Svenja geschafft, wenn sie  Liter Schokomilch und
Liter Schokomilch und  Liter Apfelsaftschorle getrunken hat? (!
Liter Apfelsaftschorle getrunken hat? (! Liter) (
Liter) ( Liter) (!
Liter) (!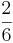 Liter)
Liter)
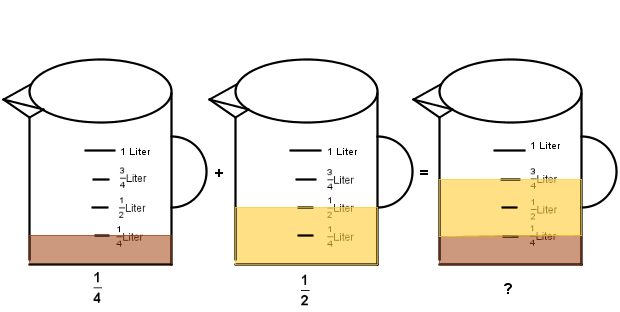
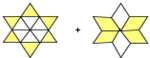
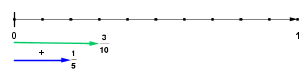
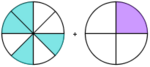
Addiere die beiden bildlich dargestellten Bruchteile und kreuze das richtige Ergebnis an!
Klicke anschließend auf prüfen!, um zu sehen, ob du Recht hast.
|
|
|
Jetzt fällt dir es bestimmt nicht schwer, den folgenden Aufgaben zwei richtige Lösungen zuzuordnen.
Vergiss nicht dein Ergebnis zu überprüfen!
Damit du immer weisst, wie du bei der Addition ungleichnamiger Brüche vorgehen musst, fülle den Lückentext mit den richtigen Wörtern aus!
Das Beispiel soll dir eine kleine Hilfe sein.
| Allgemein: |
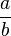 + + 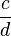 = = 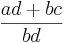
|
Beispiel von oben "Messbecher":  Liter +
Liter +  Liter =
Liter =  Liter +
Liter +  Liter =
Liter =  Liter =
Liter = 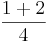 Liter =
Liter =  Liter
Liter 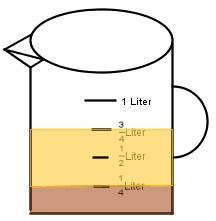


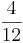 )(!
)(! )(
)( )
)


 ) (!
) (! ) (!
) (!

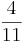 ) (
) (
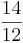
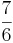
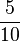

 +
+ 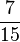
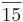
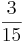 +
+ 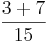 =
=