Der Satz des Thales: Unterschied zwischen den Versionen
Aus DMUW-Wiki
< Lernpfade | Satz des Thales
| Zeile 3: | Zeile 3: | ||
===Der Satz des Thales=== | ===Der Satz des Thales=== | ||
}} | }} | ||
| − | |||
<br> | <br> | ||
| + | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
| + | <br> | ||
| + | : '''Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.''' | ||
| + | <br> | ||
| + | [[Bild: ThalesClownAAeinführung1_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]] | ||
| + | <br> | ||
| + | : '''Du hast doch bei der Erarbeitung von Grundwissen verschiedene Winkel kennen gelernt, stimmts?''' | ||
| + | <br> | ||
| + | : '''Ich weiß also, dass du in der Lage bist einen spitzen von einem stumpfen Winkel zu unterscheiden!''' | ||
| + | <br> | ||
| + | : '''Auf geht's - probiere doch bitte die erste Station aus - viel Spaß!!!''' | ||
| + | <br> | ||
| + | ===Erste Station:=== | ||
| + | <br> | ||
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#8DB6CD" | ||
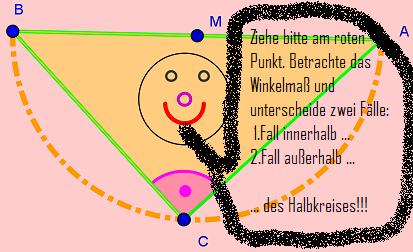
| + | | <ggb_applet height="450" width="500" showResetIcon="true" filename="widerspruchsbeweisthales_nico.ggb" /> || <br> | ||
| + | <br> !!!Ziehe am roten Punkt C. Beobachte dabei den Wert für den Winkel γ!!! | ||
| + | <br> | ||
| + | <br> | ||
| + | * 1.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C innerhalb des gelben Halbkreises befindet? | ||
| + | <br> | ||
| + | * 1.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ ist größer als 90°. Es gilt: γ > 90°</u> | ||
| + | <br> | ||
| + | * 2.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C außerhalb des gelben Halbkreises befindet? (Jedoch innerhalb der blauen Linien?) | ||
| + | <br> | ||
| + | * 2.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ ist kleiner als 90°. Es gilt: γ < 90°</u> | ||
| + | <br> | ||
| + | * 3.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C genau auf dem Halbkreis befindet? | ||
| + | <br> | ||
| + | * 3.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°</u> | ||
| + | <br> | ||
| + | * 4.Frage: Welchen Wert nimmt der Winkel γ an, wenn du das Kästchen "Punkt fixieren" anklickst? | ||
| + | <br> | ||
| + | * 4.Antwort: <u style="color:lightgrey;background:lightgrey">Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°</u> <br> | ||
| + | <br> | ||
| + | Erklärung: <u style="color:lightgrey;background:lightgrey">Es gilt: γ = 90°, weil der rote Punkt C genau auf dem Halbreis über der Strecke [AB] liegt.</u> <br> | ||
| + | |} | ||
| + | </div> | ||
<br> | <br> | ||
<br> | <br> | ||
| Zeile 129: | Zeile 167: | ||
</div> | </div> | ||
<br> | <br> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</div> | </div> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
<br> | <br> | ||
<br> | <br> | ||
Version vom 24. Juni 2009, 10:57 Uhr
 Lernpfad
|
- Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.
- Du hast doch bei der Erarbeitung von Grundwissen verschiedene Winkel kennen gelernt, stimmts?
- Ich weiß also, dass du in der Lage bist einen spitzen von einem stumpfen Winkel zu unterscheiden!
- Auf geht's - probiere doch bitte die erste Station aus - viel Spaß!!!
Erste Station:
|
|
Betrachte aufmerksam die dynamische Animation!
| Auf gehts - Löse das Quiz!
|
Betrachte aufmerksam die dynamische Animation!
Versuche den Lückentext mithilfe der dynamischen Zeichnung zu lösen.
| Wenn das Dreieck ABC bei dem Eckpunkt C rechtwinklig ist, dann liegt C auf dem Halbkreis über dem Durchmesser AB. |
In der Mathematik kommt es häufig vor, dass Satz und Kehrsatz richtig sind.
Anstelle von zwei Sätzen in Wenn-Dann-Form, wird die Formulierung "...genau dann, wenn..." verwendet,
sowohl um die Sätze zusammenzufassen als auch um die Korrektheit der Aussage zu artikulieren.
| Das Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über der Strecke AB liegt. |
Ziehe am blauen Punkt C!
Aufgabenstellung: Ordne die untenstehenden Bilder und Begriffe passend zu!!!
| Die Strecken [MA], [MB] und [MC] | sind alle gleich lang | werden mit r bezeichnet | sind der Radius des Kreises k | sind halb so lang wie der Durchmesser des Kreises k |
| Basiswinkel im Dreieck AMC | 
| |||
 |
Basiswinkel im Dreieck MBC | |||
 |
 |
|
</div>
 Merke
Der Satz des Thales: |
- Eigentlich, müsstest du jetzt doch alles verstanden haben, oder?
- Die nachstehenden Aufgaben kannst du in Absprache mit deinem Lehrer oder deiner Lehrerin bearbeiten!
Aufgabe
Arbeitsauftrag:
|
 Entstanden unter Mitwirkung von:
|
