Eigenschaften: Unterschied zwischen den Versionen

Version vom 15. Januar 2010, 16:55 Uhr

Die Definitionsmenge aller Exponentialfunktionen ist R. Es treten nur positve Funktionswerte auf. Alle Exponentialfunktionen der Form f(x) = a^x gehen durch den Punkt (0/1).
	Die Graphen von f(x) = a^x und g(x) = a^-x = 1/a^x liegen symmetrisch bezüglich der y-Achse.
Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend.
	Für 0 < a < 1 ist die positive x-Achse Asymptote.
Für a > 1 ist die negative x-Achse Asymptote.

Merke:

Die Definitionsmenge aller Exponentialfunktionen ist R.
Es treten nur positive Funktionswerte auf.
Alle Exponentialfunktionen der Form f(x) = ax gehen durch den Punkt (0/1).
Die Graphen von f(x) = ax und liegen symmetrisch bezüglich der y-Achse.
Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend.
für 0 < a < 1 ist die positive x-Achse Asymptote.
Für a > 1 ist die negative x-Achse Asymptote.

@@ Zeile 6: / Zeile 6: @@
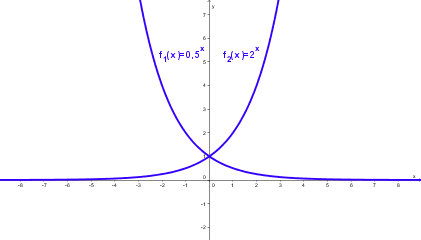
 | [[Bild:Exponentialfunktion4.png]] || '''Die Graphen von f(x) = a<sup>x</sup> und g(x) = a<sup>-x</sup> = 1/a<sup>x</sup>   liegen symmetrisch bezüglich der y-Achse.'''
 |-
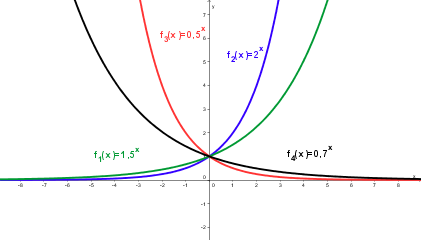
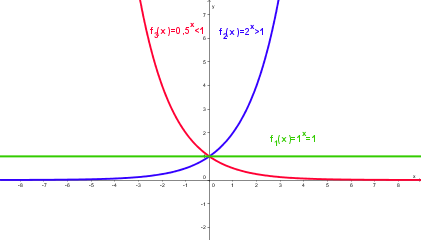
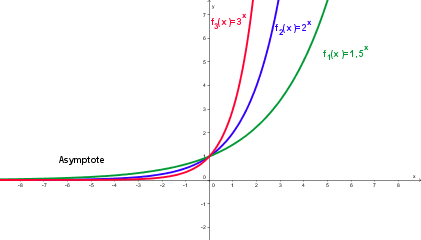
-| '''Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend.''' || [[Bild:Exponentialfunktion2.png]]
+| '''<span style="color:#ff0000">Für 0 < a < 1 ist die Exponentialfunktion monoton fallend</span>, <span style="color:#008B00">für a = 1 ist die Funktion konstant</span>, <span style="color:#00008B">für a > 1 ist sie monoton steigend.</span>''' || [[Bild:Exponentialfunktion2.png]]
 |-
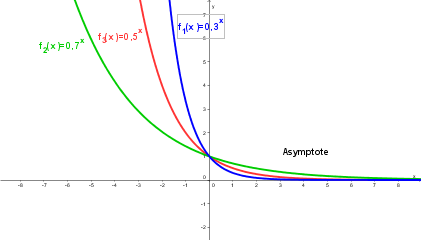
 |[[Bild:Exponentialfunktion6.png]] || '''Für 0 < a < 1 ist die positive x-Achse Asymptote.'''