Übungen: Unterschied zwischen den Versionen

Version vom 16. Januar 2010, 13:48 Uhr

Aufgabe

Zeichne die Graphen der folgenden Exponentialfunktion im Intervall [-3; 3]. Fertige, falls nötig, eine Wertetabelle an.

Aufgabe

Zeichne die Graphen der folgenden Logarithmusfunktionen für D=R⁺, indem du die entsprechenden Exponentialfunktionen an der 1.Mediane spiegelst.

@@ Zeile 2: / Zeile 2: @@
 {{Arbeit|ARBEIT=Zeichne die Graphen der folgenden Exponentialfunktion im Intervall [-3; 3].
 Fertige, falls nötig, eine Wertetabelle an.
-a) f(x) = 2x     b) f(x) = 3,5x     c) f(x) = 0,5x      d) f(x) = 3-x}}
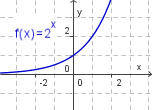
+# f(x) = 2<sup>x</sup>
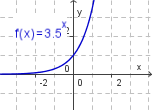
+# f(x) = 3,5<sup>x</sup>
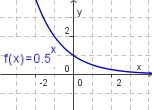
-Lösung  ausblenden
+# f(x) = 0,5<sup>x</sup>
-a)    b)     c)     d)
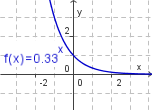
+# f(x) = 3<sup>-x</sup>}}
+<popup name="Lösung">
+{| {{Prettytable}}
+|-
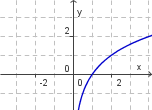
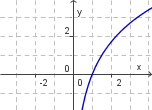
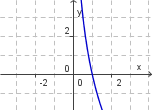
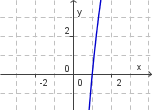
+| 1. [[Bild:bild_a.png]] || 2. [[Bild:bild_b.png]] || 3. [[Bild:bild_c.png]] || 4. [[Bild:bild_d.png]]
+|}
+</popup>
 ==Übungen 2 zur Logarithmusfunktion==
-Aufgabe: Zeichne die Graphen der folgenden Logarithmusfunktionen für D=R+, indem du die entsprechenden Exponentialfunktionen an der 1.Mediane spiegelst.
+{{Arbeit|ARBEIT=Zeichne die Graphen der folgenden Logarithmusfunktionen für D=R<sup>+</sup>, indem du die entsprechenden Exponentialfunktionen an der 1.Mediane spiegelst.
-a) f(x) = 2log x     b) f(x) = 1,5log x     c) f(x) = 0,8log x     d) f(x) = 1,1log x
-Lösung  ausblenden
-a)    b)     c)     d)
+# f(x) = log<sub>2</sub>x
+# f(x) = log<sub>1,5</sub>x
+# f(x) = log<sub>0,8</sub>x
+# f(x) = log<sub>1,1</sub>x}}
+<popup name="Lösung">
+{| {{Prettytable}}
+|-
+| 1. [[Bild:bild_2a.png]] || 2. [[Bild:bild_2b.png]] || 3. [[Bild:bild_2c.png]] || 4. [[Bild:bild_2d.png]]
+|}
+</popup>
 [http://realmath.de/Neues/Klasse10/exponentialfunktion/exponentialquiz.html Online-Übung]
 [[Media:Exp_Arbeitsblatt_Lsg.pdf]]