Einleitung: Unterschied zwischen den Versionen

Version vom 15. Januar 2010, 11:07 Uhr (Quelltext anzeigen) Stefan Baumgart (Diskussion | Beiträge) K ← Zum vorherigen Versionsunterschied		Version vom 16. Januar 2010, 18:18 Uhr (Quelltext anzeigen) Stefan Baumgart (Diskussion | Beiträge) (Inhaltsverzeichnis beigefügt) Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
		+	<div style="margin:0; margin-right:4px; margin-left:0px; border:2px solid #f4f0e4; padding: 0em 0em 0em 1em; background-color:#f4f0e4;">[[Benutzer:Stefan_Baumgart/Vorwissen|Übersicht]] - [[Benutzer:Stefan_Baumgart/Einleitung|Einleitung]] - [[Benutzer:Stefan_Baumgart/Zinseszins|Zinseszins]] - [[Benutzer:Stefan_Baumgart/Untersuchung|Untersuchung der Exponentialfunktion]] - [[Benutzer:Stefan_Baumgart/Eigenschaften|Eigenschaften der Exponentialfunktion]] - [[Benutzer:Stefan_Baumgart/Umkehrfunktion|Umkehrfunktion]] - [[Benutzer:Stefan_Baumgart/Übungen|Übungen und Lösung des Arbeitsblattes]] - [[Benutzer:Stefan_Baumgart/Rechnerische Beziehung zwischen der Exponentialfunktion und der Logarithmusfunktion|Rechnerische Beziehung zwischen der Exponentialfunktion und der Logarithmusfunktion]]
		+	</div>
		+	<br>
		+
	==Einleitung - Die Kapitalentwicklung==		==Einleitung - Die Kapitalentwicklung==

---

Version vom 16. Januar 2010, 18:18 Uhr

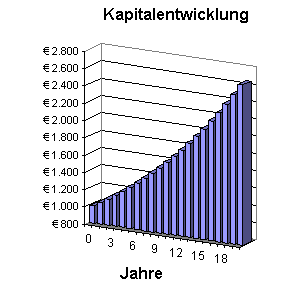
Einleitung - Die Kapitalentwicklung

Aus der Werbung einer Bank

Arbeiten Sie nicht selbst - lassen Sie Ihre Geld arbeiten

Mit der einmaligen Chance zur großartigen Kapitalvermehrung bietet Ihnen unser Institut Global Money-Invest die Möglichkeit, bei einer jährlichen Verzinsung mit 5,00% Ihr Kapital in 20 Jahren auf mehr als Zweieinhalbfache anwachsen zu lassen.

Aufgabe   Wiederhole die Formel zur Berechnung eines Kapitals nach n = 1, 2, 3, ... Jahren mit Zinseszins. Berechne, auf welchen Betrag sich ein Anfangskapital von K0 = 1.000 € bei einer Verzinsung mit p = 5% (ohne Kapitalertragssteuer KESt) in a) 10 Jahren, b) 20 Jahren anwächst.