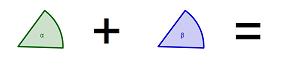|
|
| Zeile 45: |
Zeile 45: |
| | <br> | | <br> |
| | <br> | | <br> |
| − | <br>
| |
| − | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;">
| |
| − | <br>
| |
| − | [[Bild: ThalesClownSchieberegler_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
| |
| − | <br>
| |
| − | : '''Nachdem du die erste Station gemacht hast, kannst du dich jetzt der zweiten Station widmen!'''
| |
| − | <br>
| |
| − | : '''Achte zunächst auf die linke Animation und beobachte den Winkel am roten Eckpunkt!
| |
| − | <br>
| |
| − | : '''Wenn du damit fertig bist, dann schaue dir bitte dir rechte Animation an!'''
| |
| − | <br>
| |
| − | : '''Was fällt dir auf, wenn du die Winkel betrachtest?'''
| |
| − | <br>
| |
| − | : '''Um die Fragen zu beantworten, nutze bitte den Multiple-Chpoice-Test!'''
| |
| − | <br>
| |
| − | : '''Viel Spaß dabei!!!'''
| |
| − | <br>
| |
| − | ===Zweite Station:===
| |
| − | <br>
| |
| − | {| {{Prettytable}}
| |
| − | |- style="background-color:#8DB6CD"
| |
| − | | <ggb_applet height="400" width="400" showResetIcon="true" filename="OhneWinkelANIMATION_thales_nicostahl.ggb" /> || <ggb_applet height="400" width="400" showResetIcon="true" filename="ANIMATION_thales_nicostahl.ggb" />
| |
| − | |}
| |
| − | <br>
| |
| − | <big>'''Welche Aussagen über die dynamischen Animationen stimmen und welche nicht?'''</big><br>
| |
| − | <quiz display="simple">
| |
| − | {Der Winkel am roten Eckpunkt hat in der linken Animation eine andere Größe als in der rechten Animation.}
| |
| − | - Richtig
| |
| − | || In beiden Animationen hat der Winkel am roten Eckpunkt die gleiche Größe.
| |
| − | + Falsch
| |
| − |
| |
| − | {Der Winkel γ hat bei beiden Animationen stets ein Maß von 90°.}
| |
| − | + Richtig
| |
| − | - Falsch
| |
| − | || Bei beiden Animationen gilt:γ = 90°.
| |
| − |
| |
| − | {Die beiden grünen Winkel sind nie gleich groß.}
| |
| − | - Richtig
| |
| − | || Bei 45° sind beide Winkel gleich groß.
| |
| − | + Falsch
| |
| − |
| |
| − |
| |
| − | {Die Summe der beiden grünen Winkel ergibt stets das gleiche Ergebnis.}
| |
| − | + Richtig
| |
| − | - Falsch
| |
| − | || Es stimmt: Das Ergebnis lautet: 90°!
| |
| − |
| |
| − | {Die Summe der beiden grünen Winkel ist so groß wie der Winkel γ.}
| |
| − | + Richtig
| |
| − | - Falsch
| |
| − | || Es stimmt: Das Ergebnis lautet: 90°!
| |
| − |
| |
| − | {Wenn der Winkel γ nicht auf dem Kreis liegen würde, dann wäre das Winkelmaß entweder größer oder kleiner 90°.}
| |
| − | + Richtig
| |
| − | - Falsch
| |
| − | || Schaue dir die erste Station an!
| |
| − | <br>
| |
| − | <br>
| |
| − | </div>
| |
| | <br> | | <br> |
| | <br> | | <br> |
Version vom 24. Juni 2009, 15:46 Uhr
- Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.
- Du hast doch bei der Erarbeitung von Grundwissen verschiedene Winkel kennen gelernt, stimmts?
- Ich weiß also, dass du in der Lage bist einen spitzen von einem stumpfen Winkel zu unterscheiden!
- Auf geht's - probiere doch bitte die erste Station aus - viel Spaß!!!
Erste Station:
|
|
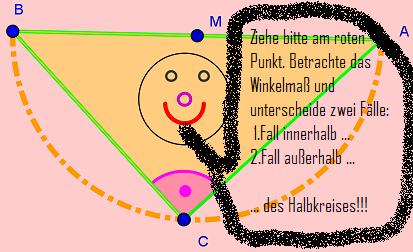
!!!Ziehe am roten Punkt C. Beobachte dabei den Wert für den Winkel γ!!!
- 1.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C innerhalb des gelben Halbkreises befindet?
- 1.Antwort: Der Winkel γ ist größer als 90°. Es gilt: γ > 90°
- 2.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C außerhalb des gelben Halbkreises befindet? (Jedoch innerhalb der blauen Linien?)
- 2.Antwort: Der Winkel γ ist kleiner als 90°. Es gilt: γ < 90°
- 3.Frage: Welchen Wert nimmt der Winkel γ an, wenn sich der rote Punkt C genau auf dem Halbkreis befindet?
- 3.Antwort: Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°
- 4.Frage: Welchen Wert nimmt der Winkel γ an, wenn du das Kästchen "Punkt fixieren" anklickst?
- 4.Antwort: Der Winkel γ beträgt dann genau 90°. Es gilt: γ = 90°
Erklärung: Es gilt: γ = 90°, weil der rote Punkt C genau auf dem Halbreis über der Strecke [AB] liegt.
|
Betrachte aufmerksam die dynamische Animation!
|
|
Auf gehts - Löse das Quiz!
Beziehe dich dabei auf die nebenstehende Animation.
Wenn die Strecke AB den Mittelpunkt M des Kreises schneidet, dann erscheint im Bild das Wort Thales.
Weiterhin gilt dann auch, dass der Winkel an der Spitze C (grün markiert) rechtwinklig ist.
Wenn das Dreieck ABC bei C ein Maß von 90° hat, so bezeichnet man die Strecke AB als Hypotenuse.
Die beiden Strecken AC und BC nennt man Katheten.
|
|
|
Versuche den Lückentext mithilfe der dynamischen Zeichnung zu lösen.
Wenn das Dreieck ABC bei dem Eckpunkt C rechtwinklig ist, dann liegt C auf dem Halbkreis über dem Durchmesser AB.
Wenn der Punkt C auf dem Halbkreis über AB liegt, dann ist das Dreieck ABC rechtwinklig bei C.
|
|
In der Mathematik kommt es häufig vor, dass Satz und Kehrsatz richtig sind.
Anstelle von zwei Sätzen in Wenn-Dann-Form, wird die Formulierung "...genau dann, wenn..." verwendet,
sowohl um die Sätze zusammenzufassen als auch um die Korrektheit der Aussage zu artikulieren.
|
Das Dreieck ABC hat genau dann bei C einen rechten Winkel, wenn die Ecke C auf dem Halbkreis über der Strecke AB liegt.
|
|
</div>
|
Der Satz des Thales:
Jedes Dreieck ∆ABC, dessen Grundseite AB dem Durchmesser eines Halbkreises entspricht und dessen Ecke C auf dem Kreisbogen liegt,
ist rechtwinklig. Den Halbkreis mit dem eingeschlossenen Dreieck bezeichnet man kurz als „Thales-Kreis“.
|
- Eigentlich, müsstest du jetzt doch alles verstanden haben, oder?
- Die nachstehenden Aufgaben kannst du in Absprache mit deinem Lehrer oder deiner Lehrerin bearbeiten!
Aufgabe 
Arbeitsauftrag:
- Konstruiere in dein Übungsheft einen Thales-Kreis.
- Schreibe die besonderen Eigenschaften eines Thales-Kreis in dein Heft.
- Füge sonstige Besonderheiten hinzu, die dir während des Bearbeitens des Lernpfades aufgefallen sind.
- Diskutiere in deiner Klassengemeinschaft über diesen Lernpfad
|