Der Satz des Thales: Unterschied zwischen den Versionen
Aus DMUW-Wiki
< Lernpfade | Satz des Thales
| Zeile 45: | Zeile 45: | ||
<br> | <br> | ||
<br> | <br> | ||
| + | <br> | ||
| + | <div style="border: 2px solid blue; background-color:#ffffff; padding:7px;"> | ||
| + | <br> | ||
| + | [[Bild: ThalesClownSchieberegler_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]] | ||
| + | <br> | ||
| + | : '''Nachdem du die erste Station gemacht hast, kannst du dich jetzt der zweiten Station widmen!''' | ||
| + | <br> | ||
| + | : '''Achte zunächst auf die linke Animation und beobachte den Winkel am roten Eckpunkt! | ||
| + | <br> | ||
| + | : '''Wenn du damit fertig bist, dann schaue dir bitte dir rechte Animation an!''' | ||
| + | <br> | ||
| + | : '''Was fällt dir auf, wenn du die Winkel betrachtest?''' | ||
| + | <br> | ||
| + | : '''Um die Fragen zu beantworten, nutze bitte den Multiple-Chpoice-Test!''' | ||
| + | <br> | ||
| + | : '''Viel Spaß dabei!!!''' | ||
| + | <br> | ||
| + | ===Zweite Station:=== | ||
| + | <br> | ||
| + | {| {{Prettytable}} | ||
| + | |- style="background-color:#8DB6CD" | ||
| + | | <ggb_applet height="400" width="400" showResetIcon="true" filename="OhneWinkelANIMATION_thales_nicostahl.ggb" /> || <ggb_applet height="400" width="400" showResetIcon="true" filename="ANIMATION_thales_nicostahl.ggb" /> | ||
| + | |} | ||
| + | <br> | ||
| + | <big>'''Welche Aussagen über die dynamischen Animationen stimmen und welche nicht?'''</big><br> | ||
| + | <quiz display="simple"> | ||
| + | {Der Winkel am roten Eckpunkt hat in der linken Animation eine andere Größe als in der rechten Animation.} | ||
| + | - Richtig | ||
| + | || In beiden Animationen hat der Winkel am roten Eckpunkt die gleiche Größe. | ||
| + | + Falsch | ||
| + | |||
| + | {Der Winkel γ hat bei beiden Animationen stets ein Maß von 90°.} | ||
| + | + Richtig | ||
| + | - Falsch | ||
| + | || Bei beiden Animationen gilt:γ = 90°. | ||
| + | |||
| + | {Die beiden grünen Winkel sind nie gleich groß.} | ||
| + | - Richtig | ||
| + | || Bei 45° sind beide Winkel gleich groß. | ||
| + | + Falsch | ||
| + | |||
| + | |||
| + | {Die Summe der beiden grünen Winkel ergibt stets das gleiche Ergebnis.} | ||
| + | + Richtig | ||
| + | - Falsch | ||
| + | || Es stimmt: Das Ergebnis lautet: 90°! | ||
| + | |||
| + | {Die Summe der beiden grünen Winkel ist so groß wie der Winkel γ.} | ||
| + | + Richtig | ||
| + | - Falsch | ||
| + | || Es stimmt: Das Ergebnis lautet: 90°! | ||
| + | |||
| + | {Wenn der Winkel γ nicht auf dem Kreis liegen würde, dann wäre das Winkelmaß entweder größer oder kleiner 90°.} | ||
| + | + Richtig | ||
| + | - Falsch | ||
| + | || Schaue dir die erste Station an! | ||
| + | <br> | ||
| + | <br> | ||
| + | </div> | ||
<br> | <br> | ||
<br> | <br> | ||
Version vom 24. Juni 2009, 15:46 Uhr
|
Lernpfad
|
- Nach dem griechischen Philosophen und Mathematiker Thales von Milet (um 600 v. Chr.) wird ein wichtiger gemeotrischer Satz bezeichnet.
- Du hast doch bei der Erarbeitung von Grundwissen verschiedene Winkel kennen gelernt, stimmts?
- Ich weiß also, dass du in der Lage bist einen spitzen von einem stumpfen Winkel zu unterscheiden!
- Auf geht's - probiere doch bitte die erste Station aus - viel Spaß!!!
Erste Station:
|
|
- Nachdem du die erste Station gemacht hast, kannst du dich jetzt der zweiten Station widmen!
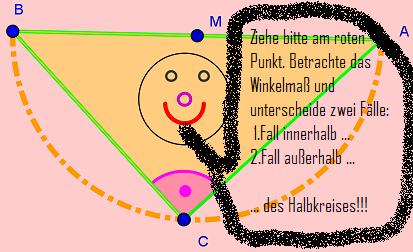
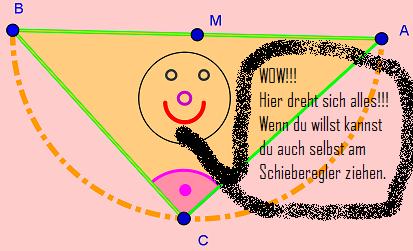
- Achte zunächst auf die linke Animation und beobachte den Winkel am roten Eckpunkt!
- Wenn du damit fertig bist, dann schaue dir bitte dir rechte Animation an!
- Was fällt dir auf, wenn du die Winkel betrachtest?
- Um die Fragen zu beantworten, nutze bitte den Multiple-Chpoice-Test!
- Viel Spaß dabei!!!
Zweite Station:
Welche Aussagen über die dynamischen Animationen stimmen und welche nicht?