Eigenschaften: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(Anweisung eingefügt) |
K |
||
| Zeile 21: | Zeile 21: | ||
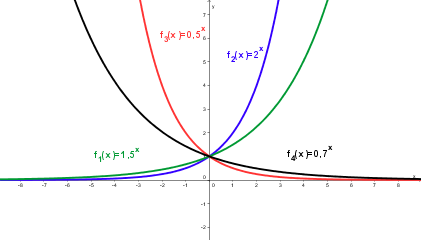
* Die Definitionsmenge aller Exponentialfunktionen ist R. | * Die Definitionsmenge aller Exponentialfunktionen ist R. | ||
* Es treten nur positive Funktionswerte auf. | * Es treten nur positive Funktionswerte auf. | ||
| − | * Alle Exponentialfunktionen der Form f(x) = | + | * Alle Exponentialfunktionen der Form f(x) = a<sup>x</sup> gehen durch den Punkt (0/1). |
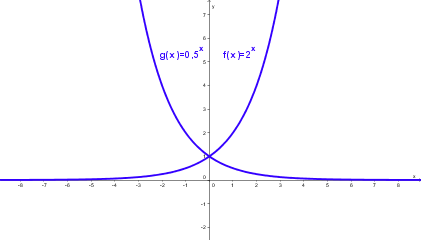
| − | * Die Graphen von f(x) = | + | * Die Graphen von f(x) = a<sup>x</sup> und g(x) = a<sup>-x</sup> = 1/a<sup>x</sup> liegen symmetrisch bezüglich der y-Achse. |
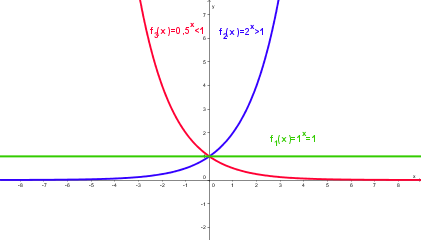
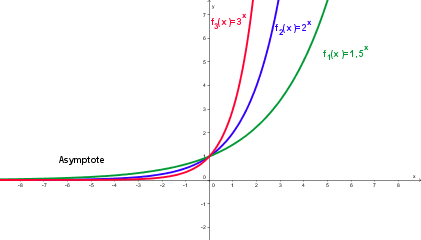
* Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend. | * Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend. | ||
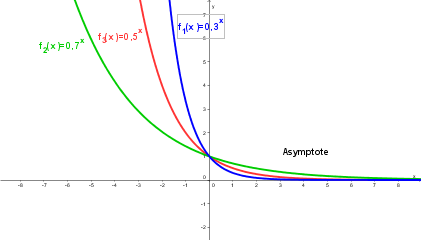
* für 0 < a < 1 ist die positive x-Achse Asymptote. | * für 0 < a < 1 ist die positive x-Achse Asymptote. | ||
Version vom 20. Januar 2010, 14:47 Uhr
Übersicht - Einleitung - Zinseszins - Untersuchung der Exponentialfunktion - Eigenschaften der Exponentialfunktion - Umkehrfunktion - Übungen und Lösung des Arbeitsblattes - Rechnerische Beziehung zwischen der Exponentialfunktion und der Logarithmusfunktion
Eigenschaften der Exponentialfunktion
| Die Definitionsmenge aller Exponentialfunktionen ist R. Es treten nur positve Funktionswerte auf. Alle Exponentialfunktionen der Form f(x) = ax gehen durch den Punkt (0/1). | 
|
 |
Die Graphen von f(x) = ax und g(x) = a-x = 1/ax liegen symmetrisch bezüglich der y-Achse. |
| Für 0 < a < 1 ist die Exponentialfunktion monoton fallend, für a = 1 ist die Funktion konstant, für a > 1 ist sie monoton steigend. | 
|
 |
Für 0 < a < 1 ist die positive x-Achse Asymptote. |
| Für a > 1 ist die negative x-Achse Asymptote. | 
|
 Merke:
|
Löse an dieser Stelle das Arbeitsblatt zum Lernpfad
