Quadratische Funktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 1: | Zeile 1: | ||
=Quadratische Funktionen= | =Quadratische Funktionen= | ||
| − | |||
| − | Ihr Funktionsterm hat die Form '''ax²'''. Wie wir schon festgestellt haben, unterscheiden sich die Graphen quadratischer Funktionen stark von den Graphen linearer Funktionen. | + | {|border="0" cellspacing="0" cellpadding="4" |
| + | |align = "left" width="450"|Ihr Funktionsterm hat die Form '''ax²'''. Wie wir schon festgestellt haben, unterscheiden sich die Graphen quadratischer Funktionen stark von den Graphen linearer Funktionen. | ||
<br /> | <br /> | ||
Hier erfährst du alle wichtigen Merkmale der quadratischen Funktion: | Hier erfährst du alle wichtigen Merkmale der quadratischen Funktion: | ||
| Zeile 14: | Zeile 14: | ||
}} | }} | ||
<br /> | <br /> | ||
| + | |||
| + | |||
| + | === Merksatz: (Rein-)Quadratische Funktionen === | ||
| + | |||
| + | {|border="0" cellspacing="0" cellpadding="4" | ||
| + | |align = "left" width="450"|Die Funktionen, die wir bis jetzt betrachtet haben, weisen eine Gemeinsamkeit auf: Ihr Funktionsterm hat die Form '''ax²'''. Sie zählen daher zu den '''quadratischen Funktionen'''. Die Graphen quadratischer Funktionen unterscheiden sich stark von den Graphen linearer Funktionen. | ||
| + | <br /> | ||
| + | {{Merksatz|MERK= Die Graphen von Funktionen mit der Funktionsgleichung <math>f(x)=ax^2</math> heißen '''Parabeln'''. | ||
| + | |||
| + | Sie sind '''symmetrisch zur y-Achse.''' Der Punkt <math>S(0\!\,|\!\,0)</math> heißt '''Scheitel der Parabel''' und ist der tiefste Punkt. | ||
| + | |||
| + | Ist <math>a = 1</math> heißt der Graph '''Normalparabel'''. | ||
| + | }} | ||
| + | <br /> | ||
| + | |||
| + | |||
| + | |||
| + | |width=20px| | ||
| + | |valign="top"|GEOGEBRA-APPLET | ||
| + | |||
| + | |||
| + | |} | ||
Version vom 13. Februar 2010, 01:36 Uhr
Quadratische Funktionen
| Ihr Funktionsterm hat die Form ax². Wie wir schon festgestellt haben, unterscheiden sich die Graphen quadratischer Funktionen stark von den Graphen linearer Funktionen.
Merksatz: (Rein-)Quadratische Funktionen
|

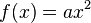 heißen Parabeln.
heißen Parabeln.
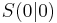 heißt Scheitel der Parabel und ist der tiefste Punkt.
heißt Scheitel der Parabel und ist der tiefste Punkt.
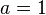 heißt der Graph Normalparabel.
heißt der Graph Normalparabel.

