Flächeninhalt ebener Figuren: Unterschied zwischen den Versionen
(→3. Klassenzimmer streichen: Rückwand Bild eingefügt und Aufgabenstellung erweitert) |
(→3. Klassenzimmer streichen: Bild eingefügt für Lösungsvorschläge) |
||
| Zeile 40: | Zeile 40: | ||
<br> | <br> | ||
:Du findest hier ein paar Lösungsvorschläge: | :Du findest hier ein paar Lösungsvorschläge: | ||
| − | {{Lösung versteckt|. | + | {{Lösung versteckt| |
| + | [[Bild:Ebert_LösungsvorschlägeWand.jpg|center]]}} | ||
<br> | <br> | ||
'''Hast Du mehr Ideen gefunden?? Prima!''' | '''Hast Du mehr Ideen gefunden?? Prima!''' | ||
<br> | <br> | ||
'''Aufgabenstellung:''' | '''Aufgabenstellung:''' | ||
| − | Zeige, warum im Lösungsvorschlag 1, 3 und | + | Zeige, warum im Lösungsvorschlag '''1, 3, 7 und 8''' jeweils genau die Hälfte grün bzw. gelb gestrichen wird. '''Begründe mit dem, was Du bisher über Flächeninhalte gelernt hast.''' |
{{Lösung versteckt|......}} | {{Lösung versteckt|......}} | ||
Version vom 29. Juni 2009, 15:52 Uhr
Entdecke auf dieser Seite, wie man die Flächeninhalte ebener Figuren berechnet!!
1.Wiederholung: Flächeninhalt von Rechtecken und Quadraten
Das solltest Du also wissen
2.Das ist ja die Höhe!!: Höhen ebener Figuren
2.1 Höhen im Parallelogramm
2.2 Höhen im Dreieck
2.2 Höhen im Trapez
Aufgabensammlung
3. Klassenzimmer streichen
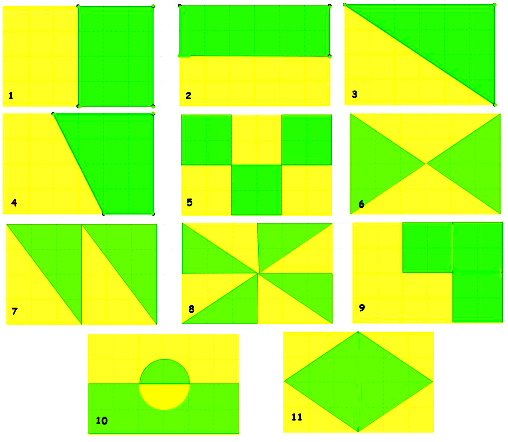
- Eine Schulklasse hat sich entschieden die Rückwand des Klassenzimmers neu zu streichen. Da die Mädchen gelb und die Jungen grün streichen wollen, haben sie sich geeinigt die Rückwand jeweils in der Hälfte der Farben zu streichen.
- Hilf der Klasse bei den Designvorschlägen.
- Hier siehst Du die Rückwand des Klassenzimmers. Sie ist 4 Meter hoch und 6 Meter breit.
Wieviele Vorschläge hast Du? Übertage das Rechteck in Dein Heft und sei kreativ! Aber achte auf die Aufgabenstellung!
- Du findest hier ein paar Lösungsvorschläge:
Hast Du mehr Ideen gefunden?? Prima!
Aufgabenstellung:
Zeige, warum im Lösungsvorschlag 1, 3, 7 und 8 jeweils genau die Hälfte grün bzw. gelb gestrichen wird. Begründe mit dem, was Du bisher über Flächeninhalte gelernt hast.
4.Flächeninhalt Parallelogramm
4.1 Einstieg
| Verschiebe das Rechteck und beobachte was passiert! Bearbeite dazu die folgenden Fragen:
Die Breite des Rechtecks entspricht der Höhe des Parallelogramms.
|
4.2 Sicherung
Übertrage folgenden Abschnitt in Dein Heft.Fülle zunächst die Lücken aus:
| Merke: Länge(Rechteck) = Grundseite (Parallelogramm) Der Flächeninhalt des Parallelogramms ist definiert als: |
h mit
g als Grundseite
4.3 Vertiefen und Erweitern
Bitte bearbeite die folgenden Aufgaben.
| Erkläre, warum die abgebildeten Parallelogramme den gleichen Flächeninhalt, wie das rote Rechteck haben.
Du kannst die Parallelogramme an den farbigen Eckpunkten L, I und N ziehen.
Überlege dir zunächst, warum die Parallelogramme den gleichen Flächeninhalt haben könnten. |
- Will man die Höhe im nächsten Parallelogramm einzeichnen, liegt diese außerhalb.
Wie könnte man für dieses spezielle Parallelogramm die Formel für den Flächeninhalt von Parallelogrammen trotzdem beweisen?
Aufgabenstellung:
|
:Eine weitere Lösungsidee ist in der nächsten Darstellung verborgen:
Aufgabenstellung:
|
| Merke: Zur Berechnung der Flächeninhaltsformel kann |
jede Seite des Parallelogrammes als Grundseite und die zugehörige Höhe genommen werden. |
