Calculators, Power Series and Chebyshev Polynomials: Unterschied zwischen den Versionen

Version vom 23. April 2010, 04:05 Uhr

Of all the familiar functions, such as trigonometric, exponential and logarithmic functions, surely the simplest to evaluate are polynomial functions. The purpose of this article is to introduce the concept of a power series, which can be thought of in the first place as a polynomial function of infinite degree. In particular, we will deduce a series for 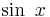and will see how to improve on the the most straightforward way of approximating its values. This simplest way uses the polynomials obtained by truncating the power series. The improvement will involve Chebyshev polynomials, which are used in many ways for a similar purpose and in many other applications, as well. When a calculator gives values of trigonometric or exponential or logarithmic functions it is doing so by evaluating polynomial functions that are sufficiently good approximations. (For trigonometric functions, the CORDIC algorithm is in fact often the preferred method of evaluation---the subject of another article here, perhaps.)

In the spirit of Felix Klein, there will be some reliance on a graphical approach.

Manipulations with geometric series

The geometric series 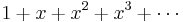is the simplest power series. The sum of the series exists when 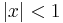. In that case

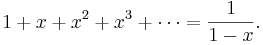
The general form of a \emph{power series} is \[ a_0+a_1x+a_2x^2+a_3x^3+\cdots, \] so the geometric series above is a power series in which all the coefficients $a_0$, $a_1$, $a_2$, \ldots, are equal to 1. In this case, since the series converges to $1/(1-x)$ when $|x|<1$, we say that the function $f$, where \[ f(x)=\frac1{1-x}, \quad |x|<1, \] has the series expansion $1+x+x^2+x^3+\cdots$, or that $f$ is represented by this series. We are interested initially to show some other functions that can be represented by power series.