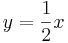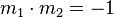Exkurs Lineare Funktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 44: | Zeile 44: | ||
===Berechnungen zu linearen Funktionen=== | ===Berechnungen zu linearen Funktionen=== | ||
<quiz> | <quiz> | ||
| − | { <popup name="Tipp"> | + | {[[Bild:Peter_Fischer_Papier.png|40px]] <popup name="Tipp"> |
Gleichsetzen der Gleichungen für Schnittpunkte. | Gleichsetzen der Gleichungen für Schnittpunkte. | ||
Um m und t berechnen zu können musst du ein Gleichungssystem aufstellen, in dem du A und B in <math>y=mx+t</math> einsetzt! </popup> | Um m und t berechnen zu können musst du ein Gleichungssystem aufstellen, in dem du A und B in <math>y=mx+t</math> einsetzt! </popup> | ||
Version vom 26. Mai 2010, 10:47 Uhr
Inhaltsverzeichnis |
Lineare Funktionen
Geraden kennst du bereits aus der achten Klasse, hier sind nochmal die wichtigsten Eigenschaften zusammengefasst. {{#slideshare:linear-100526023200-phpapp02}}
Auch zu linearen Funktionen solltest du nun ein paar Aufgaben erledigen.
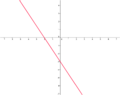
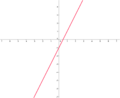
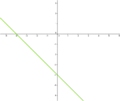
Gleichungen & Graphen zuordnen
Sortierung nach Eigenschaften
Sortiere die Funktionsgleichungen in ihre Kategorien
| Parallele Geraden | y=0,5x | 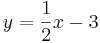 |
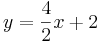 |
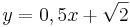
|
| Senkrechte Geraden | 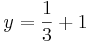 |
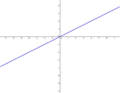
y=3x-4 | ||
| Parallele zur y-Achse | x=3 | x=-4,25 | ||
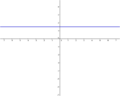
| Parallele zur x-Achse | y=5 | y=-9 | 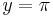
|
Berechnungen zu linearen Funktionen
Weiter gehts zu Exkurs Quadratische Funktionen
Potenzen und Potenzfunktionen
LERNPFAD | Potenzen und Potenzfunktionen | Exkurs Lineare Funktionen | Exkurs Quadratische Funktionen | Potenzfunktionen | Potenzfunktoinsabbildungen