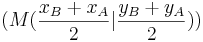Potenzfunktionen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 28: | Zeile 28: | ||
*Tabellarisiere f für <math>x \in \{0,5; 1; 2; 3; 4; 5; 6\}</math> und zeichne den Graphen in ein Koordinatensystem. | *Tabellarisiere f für <math>x \in \{0,5; 1; 2; 3; 4; 5; 6\}</math> und zeichne den Graphen in ein Koordinatensystem. | ||
| − | Für die Zeichnung: <math>1 LE = 1 cm; -3 \leq x \leq 7; -11 \leq y \leq 3</math> | + | Für die Zeichnung: <math>1 LE \widehat{=} 1 cm; -3 \leq x \leq 7; -11 \leq y \leq 3</math> |
<div class="lueckentext-quiz"> | <div class="lueckentext-quiz"> | ||
| Zeile 55: | Zeile 55: | ||
*Mittelsenkrechte über [AB] errichten, denn alle Punkte dieser Linie haben die gleiche Entfernung zu A und zu B. | *Mittelsenkrechte über [AB] errichten, denn alle Punkte dieser Linie haben die gleiche Entfernung zu A und zu B. | ||
*C<sub>3</sub> ist der Schnittpunkt der Mittelsenkrechten und dem Funktionsgraphen von f. | *C<sub>3</sub> ist der Schnittpunkt der Mittelsenkrechten und dem Funktionsgraphen von f. | ||
| − | RECHNUNG: | + | RECHNUNG:[[Bild:Peter_Fischer_Formelsammlung.png]] |
* Steigung der Geraden AB ausrechnen <math>m=\frac{y_B-y_A}{x_B-x_A}</math> | * Steigung der Geraden AB ausrechnen <math>m=\frac{y_B-y_A}{x_B-x_A}</math> | ||
* Steigung der Mittelsenkrechten mit <math>m_1 \cdot m_2=-1 </math> ermittlen | * Steigung der Mittelsenkrechten mit <math>m_1 \cdot m_2=-1 </math> ermittlen | ||
Version vom 27. Mai 2010, 15:27 Uhr
Potenzfunktionen
{{#slideshare:potenzfunktion-100520132023-phpapp01}}
Hier eine Aufgabe, die bereits Mathematik aus verschiedenen Bereichen verbindet und Prüfungsaufgaben ähnelt.
Aufgabe mit einer Hyperbel
Gegeben ist die Funktion f ,mit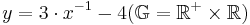
- Ermittle die nach y aufgelöste Gleichung der Umkehrfunktion f-1 zu f.
- Gib die Wertemenge der Funktion an.
- Tabellarisiere f für
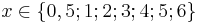 und zeichne den Graphen in ein Koordinatensystem.
und zeichne den Graphen in ein Koordinatensystem.
Für die Zeichnung: 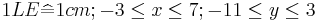
Ordne den x-Werten die passenden Funktionswerte zu!
| x | 0,5 | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 2,00 | -1,00 | -2,50 | -3,00 | -3,25 | -3,40 | -3,50 |
Hier ist ein Applet zur anschaulichen Darstellung![]()
- Die Punkte
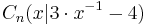 auf dem Graphen f sind zusammen mit den Punkten A(-2|-2) und B(1|-10) jeweils die Eckpunkte von Dreiecken ABCn.
auf dem Graphen f sind zusammen mit den Punkten A(-2|-2) und B(1|-10) jeweils die Eckpunkte von Dreiecken ABCn.
Zeichne das Dreieck ABC1 für x=1 und das Dreieck ABC2 für x=4 in das Koordinatensystem ein.
- Unter den Dreiecken ABCn gibt es ein gleichschenkliges Dreieck ABC3 mit der Basis [AB]. Zeichne dieses Dreieck in das Koordinatensystem ein und berechne die Koordinaten des Punktes C3.
- Es gibt ein x für das ein Dreieck ABC4 den Flächeninhalt
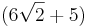 FE besitzt. Berechne dieses x.
FE besitzt. Berechne dieses x.
[Teilergebnis: 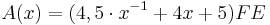 ]
]
Weiter gehts zu Potenzfunktionsabbildungen
Potenzen und Potenzfunktionen

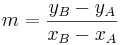
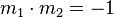 ermittlen
ermittlen