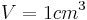Volumen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(→Volumen von Quader und Würfel) |
|||
| Zeile 1: | Zeile 1: | ||
| − | =='''<u>Volumen von | + | =='''<u>Volumen von Würfel und Quader</u>'''== |
<br> | <br> | ||
<br> | <br> | ||
| Zeile 8: | Zeile 8: | ||
| width="650" | | | width="650" | | ||
<div style="padding:10px;background:#ffffff;border:1px ;"> | <div style="padding:10px;background:#ffffff;border:1px ;"> | ||
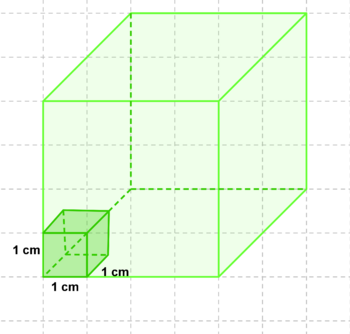
| − | ==='''<u> | + | ==='''<u>Einheitswürfel</u>'''=== |
<br> | <br> | ||
<br> | <br> | ||
| Zeile 17: | Zeile 17: | ||
|| [[Bild:Einheitswürfel.png|350px]] | || [[Bild:Einheitswürfel.png|350px]] | ||
|} | |} | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | {| | ||
| + | |- | ||
| + | | width="650" | | ||
| + | <div style="padding:10px;background:#ffffff;border:1px ;"> | ||
| + | ==='''<u>Volumen vom Würfel</u>'''=== | ||
| + | <br> | ||
| + | <br> | ||
| + | '''Da wir nicht immer alle Einheitswürfel abzählen können, da es bei manchen zu viele sind, brauchen wir eine Formel die uns beim Berechnen des Volumens helfen soll. Um diese zu erhalten sollen uns die zwei folgenden Bilder helfen.''' | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | {| | ||
| + | |- | ||
| + | | width="650" | | ||
| + | <div class="multiplechoice-quiz"> | ||
| + | <div style="padding:10px;background:#ffffff;border:1px ;"> | ||
| + | '''Hier rechts im Bild haben wir vorne a Einheitswürfel nebeneinander liegen. Und diese Reihe haben wir nach hinten weg insgesamt a mal liegen. Kannst du sagen wie groß diese untere Fläche ist?''' | ||
| + | </div> | ||
| + | (a·a m²) (!a+a m²) (!a m²) (!2·a m²) | ||
| + | </div> | ||
| + | |} | ||
| + | |||
Version vom 11. Juli 2010, 21:19 Uhr
Volumen von Würfel und Quader
Volumen vom Würfel
|