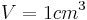Volumen: Unterschied zwischen den Versionen
Aus DMUW-Wiki
(→Volumen von Würfel und Quader) |
(→Volumen von Würfel und Quader) |
||
| Zeile 48: | Zeile 48: | ||
|} | |} | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | {| | ||
| + | |- | ||
| + | | width="650" | | ||
| + | <div style="padding:10px;background:#ffffff;border:1px ;"> | ||
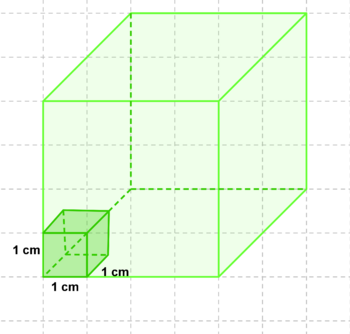
| + | '''Wir wissen nun, dass unsere untere Fläche a m² groß ist. Diese Fläche haben wir, wie du rechts im Bild sehen kannst auch a mal nach oben hin.''' | ||
| + | </div> | ||
| + | <div class="multiplechoice-quiz"> | ||
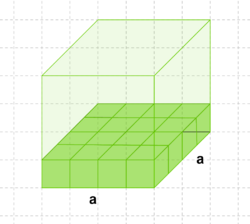
| + | Kannst du nun auch sagen wie groß dieses Volumen ist? (a²·a m³) (!a²·a m²) (!a²+a m³) (!2·a² m³) | ||
| + | |||
| + | Du weißt nun wie groß a ist. Kannst du sagen wie groß das Volumen an diesem speziellen Würfel ist? (!32 m³) (!20 m³)(!64 m²) (64 m³) | ||
| + | </div> | ||
| + | || [[Bild:Würfel4Einheitswürfel.png|250px]] | ||
| + | |} | ||
| + | |} | ||
[[../|Hier geht es zurück]] | [[../|Hier geht es zurück]] | ||
[[Benutzer:Nadine Kürten|Hier geht es zurück]] | [[Benutzer:Nadine Kürten|Hier geht es zurück]] | ||
Version vom 11. Juli 2010, 21:38 Uhr
Volumen von Würfel und Quader