Lineare Funktionen (Stefan Gaubitz): Unterschied zwischen den Versionen
Aus DMUW-Wiki
| Zeile 6: | Zeile 6: | ||
Verändere den Paramter m beliebig. | Verändere den Paramter m beliebig. | ||
| − | <ggb_applet width="1239" height="894" version="3.2" ggbBase64=" | + | <ggb_applet width="1239" height="894" version="3.2" ggbBase64="UEsDBBQACAAIAI+87DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1srVVNb9QwED3TX2H5BEjtJrssaqWkFRQJVSpwWOiBm5NMElPHjmynzfbXM2Mnu8sCUg892Z6ZzLx585HsauwUewDrpNE5T88SzkCXppK6yfng69NzfnV5kjVgGiisYLWxnfA5X50tOckHeXnyKnOteWRCBZM7CY85r4VywJnrLYjKtQD+D7kYRqmksNtvxS8ovdsropMb3Q8YxdsBZWVX3Uo3PxchYK+k/yQfZAWWKVPm/P0aoePtDqyXpVA5f5dEyTLnyyMlilakbY2VT0Z7Mt87r1HCmJNPgIwsSZYtQqIZDKWSlRSakgk40IixR1n5lmxXF+gTZNMi2POLZXRXGmOrzdZ56Nj4E6xBsMk5Mb2Nr3W6opdDYBhxnQTV4Su4gYcNeI91cUyM4GZyGiurHXv0uHEfjdqLeiO1vxa9H2yo6WoSbfyW/GMoS3g/6EbBJFsi5S2U94UZN5GEVXT9fduHTwKeork2ylhmid41GkxnEc9gQ0B3VkmwSYLF5IOc7vQpEkYW4SziGayU1BHalHg6Z50mcxjpGAmIRWzFmRslCsDKcjZo6W/nB3bA/ZRpGu2/Dl2BI3DYAzuX6Qu5zBZHzZPdg9WgYodoLOxgBsceqBVj6QKOCkrZ4TMqJkIEFesHAojSChoLM+44P5GuoE0Ou/BInC1mEITBIdbS4yLAfDzlQnPqcUZyvvFQC80+i6GQ/omzSnjS00go6ADnxYfe0EMHVpY7njpOsTHgMIVN53YOK8OE6T/idl8EVP+ne3BP9K3A21k69YjY4iY4TDh4+2KqOfAUVoWV0UncdqdrmrROjDhmdBOFM2rwsCmRTn1rSuHDVozo5iFPwnziN6v0IkwqbRq61HKE/dz9e7XsW9m32DManAvz5g8nS2gseagD7ow+JombFMh72NCzNesx7TDVu47BNosFodKMuH0dbfaZ2hq3+4ge69fjG5azjr1lI2eLv8pYDzo0At9/+Gz0L1XY5JmFTZ7N7CE3i8N+Dwt++sNd/gZQSwcI93yZ6PkCAAATBwAAUEsBAhQAFAAIAAgAj7zsPPd8mej5AgAAEwcAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAAzAwAAAAA=" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> |
| − | + | ||
Aktuelle Version vom 12. Juli 2010, 22:55 Uhr
Gegeben ist die Funktion f(x) = m·x + t mit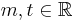 
.
Aufgabe 1
Zunächst ist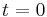 
und die Funktion lautet f(x) = m·x.
Verändere den Paramter m beliebig.
Welche Beobachtung machst du?
Was passiert bei einem negativen m?
Für was steht m in der Funktionsgleichung?
Aufgabe 2
Nun ist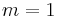 
und die Funktion lautet 
.
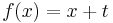Verändere den Parameter t beliebig.
Welche Beobachtung machst du? Welchen Schnittpunkt des Graphen kann man mithilfe von t direkt in der Funktion selbst ablesen?
Aufgabe 3
Abschließend sind sowohl m und t variabel. Verändere beide Parameter beliebig. Bestätigen sich deine Vermutungen aus Aufgabe 1 und 2?
