Übungsaufgaben zum Satz des Thales: Unterschied zwischen den Versionen

Version vom 9. Juli 2009, 08:27 Uhr

Lernpfad

Übungsaufgaben zum Satz des Thales

Ich bin der Thales-Clown

Erinnerst du dich noch an die Beispiele im letzten Lernpfad?

Auf geht's - probiere doch gleich einmal die erste Station aus!!!

Erste Station:

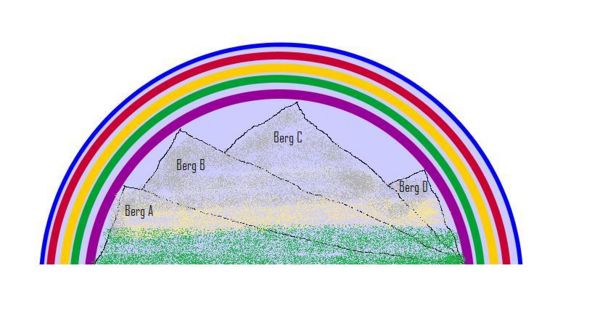
Hier siehst du einen schönen Regenbogen mitten in einer Berglandschaft auf dem Planet Phantasia.

Berglandschaft mit Regenbogen

Welcher Gipfel dieser Berglandschaft ist am spitzesten?

Frage a): Hast du eine Idee, wie groß der Winkel am Gipfel von Berg A sein könnte?

Antwort a): Der Berg A hat am Gipfel ein Winkelmaß von: 90°

Frage b): Haben die Winkel der Berge A,B,C,D, die den Regenbogen berühren eine Gemeinsamkeit?

Antwort b): Alle Winkel, die den Regenbogen berühren sind gleich groß.

Ich bin der Thales-Clown

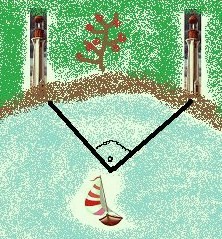
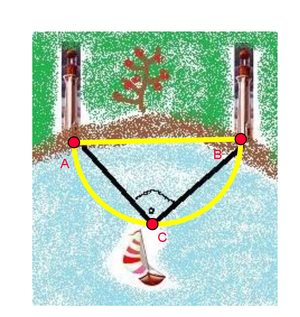
Schaue dir einmal das Bild mit dem Segelschiff an!

Auf geht's - probiere doch gleich einmal die zweite Station aus!!!

Zweite Station:

Ein Matrose und sein Kapitän segeln zusammen am Meeresufer entlang und entdecken zwei Leuchttürme unter einem Winkel von 90°.

Leuchttürme mt Segelschiff

Überlegungen:

Welche Position könnte denn das Segelschiff haben?

Stehen die beiden Leuchttürme zueinander in Beziehung?

Könnte es sich um eine geometrische Figur handeln, wenn man Objekte miteinander verbindet?

Was bedeutet die Angabe: "unter einem Winkel von 90°" Was kannst du daraus schließen?

Auf geht's - löse den Lückentext:

Zwei Standorte auf dem Festland werden mit A und B bezeichnet. In der Zeichnung sind das die .
Das Objekt im Meer, also das wird mit dem Buchstaben C versehen. Nun verbinden wir die Punkte A,B und C miteinander und erhalten ein .
Der Winkel an der beträgt 90°.
Der Matrose und sein Kapitän segeln mit dem Schiff vom linken zum rechten Leuchtturm genau so, dass der Winkel bei C stets ein Maß von 90° hat.
Dies lässt vermuten, dass die gefahrene Route einen ergibt.
Der Durchmesser dieses Halbkreises wird durch die gezeigt.

LeuchttürmeHalbkreisSegelschiffStrecke ABrechtwinkliges DreieckSpitze C

Ich bin der Thales-Clown

Du hast die zweite Station geschafft? - Naja, dann wird die dritte Station ein Kinderspiel für dich!!!

Auf geht's - probiere doch gleich einmal die dritte Station aus!!!

Dritte Station:

Anhand dieser Zeichnung kannst du den Zusammenhang erkennen, den du im Lückentext erarbeiten solltest.

Leuchttürme mit Segelschiff "Thales"

Frage a): Wenn das Schiff zum Leuchtturm B fährt, unter welchem Winkel blicken der Matrose und der Kapitän aufs Festland?

Antwort a): Die beiden Seeleute betrachten es von einem 90° Winkel aus.

Frage b): Wenn aber das Schiff zum Leuchtturm A fährt, unter welchem Winkel blicken dann die Schiffsleute aufs Festland ?

Antwort b): Dann betrachten es die Seemänner von einem 90° Winkel aus.

Daraus können wir schließen, dass der Winkel bei C immer (nkliewihctrg) ist,
wenn die Strecke von Leuchtturm A zu Leuchtturm B der (husedscerrm) des (bkselshriae) über der Strecke AB ist.

Ich bin der Thales-Clown

Jetzt versuchen wir das Ganze ein bisschen abstrakter anzugehen, ok?

Orientiere dich einfach bei der kommenden Aufgabe an die Fragestellungen bei Station II und Station III.

Ich bin mir sicher, dass du es kannst!

Auf geht's - viel Spaß beim Bearbeiten des Lückentextes!!!

Fülle die Lücken, indem du die passenden Begriffe zu den Feldern ziehst (mit der linken Maustaste zur Lücke ziehen und fallenlassen).

Vierte Station:

Wir wollen diesen Sachverhalt nun mathematisch untersuchen und dazu gehen wir davon aus,
dass das in der Zeichnung ersichtliche Dreieck einen Winkel bei C aufzeigt.
Also sind die gleich weit von entfernt,
liegen somit auf dem um M,
der zugleich von der ist.
Das heißt, wenn das bei der rechtwinklig ist,
dann liegt C auf dem über der Strecke AB.
Die Strecke AB ist zudem auch der des .

rechtenPunkte A, B und CMittelpunktStrecke ABTHALES-KREISESDreieck ABCKreisMDurchmesserEcke CHalbkreis

Ich bin der Thales-Clown

Fünfte Station!

Hier hast du eine Wiederholung zum Satz des Thales, bei der du die Winkelbeziehungen zueinander wiederholen kannst!

Beziehe dich bei der Beantwortung der Aufgaben auf die nebenstehende Zeichnungen!!!

Auf geht's - viel Spaß beim Multiple-Choice!

Ich bin der Thales-Clown

So - jetzt fassen wir zusammen, was wir in den letzten fünf Stationen eingeübt und wiederholt haben.

Schlagt bitte euer Arbeitsheft auf und tragt den Merke-Text ein!

Merke

Der Satz des Thales:

Eine mögliche Kurzformulierung lautet:

Alle Winkel am Halbkreisbogen sind rechte Winkel.

Eine andere exakte Formulierung heißt:

Konstruiert man ein Dreieck aus den beiden Endpunkten des Durchmessers eines Halbkreises (Thaleskreis)

und einem weiteren Punkt dieses Halbkreises, so erhält man immer ein rechtwinkliges Dreieck.

Oder anders ausgedrückt lautet der Satz:

Liegt der Punkt C eines Dreiecks ABC auf einem Halbkreis über der Strecke AB, dann hat das Dreieck bei C immer einen rechten Winkel.

Die Umkehrung des Thales-Satzes ist ebenfalls richtig:

Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt immer in der Mitte der Hypotenuse,

also der (längsten) Seite des Dreiecks, die dem rechten Winkel gegenüber liegt.

Hier erhälst du zusätzliche Informationen:Satz des Thales

Ich bin der Thales-Clown

Hast du Lust Fragen zu beantworten, die den Stoff aller drei Lernpfade beinhalten?

Ich bin mir sicher, dass du es kannst!

Auf geht's - viel Spaß beim Bearbeiten des Kreuzworträtsels!!!

Sechste Station:

Beim Klick auf die Ziffern im Kreuzworträtsel öffnet sich ein Eingabefeld zum Eintragen.

						6







					1
10			3

							9
				5

4

					7

	2	8

Benutzen Sie zur Eingabe die Tastatur. Eventuell müssen sie zuerst ein Eingabefeld durch Anklicken aktivieren.

Senkrecht: Diese Winkel ergänzen sich zu 180° und so bezeichnet man das Paar gegenüberliegender Winkel.1; Die Länge des Radius mit zwei multipliziert.6; Kurze Bezeichnung für einen Winkel α kleiner 90°.8; Kurze Bezeichnung für einen Winkel α ist gleich 90°.9; Der Name des berühmten Mathematikers, der in den Lernpfaden besprochen wurde.10

Waagrecht: Bezeichnung für die beiden maßgleichen Winkel in einem gleichschenkligen Dreieck.2; Bezeichnung für die längste Seite eines rechtwinkligen Dreiecks.3; Kurze Bezeichnung für einen Winkel α größer 90°.4; Im Dreieck ergibt diese genau 180°.5; Bezeichnung für die beiden Seiten des rechtwinkligen Dreiecks, die den rechten Winkel bilden.7

Ich bin der Thales-Clown

Hier findest du Wörter, die du beim Bearbeiten aller drei Lernpfade kennengelernt hast.

Ich bin fest davon überzeugt, dass du es schaffst!

Auf geht's - viel Spaß beim Bearbeiten dieser Aufgabe!!!

Waagrecht und senkrecht, gefundene Wörter werden grün markiert.

Die Lösungen können senkrecht, waagrecht und diagonal verlaufen.

Siebte Station:

H

O

U

J

T

X

Q

C

N

A

S

J

P

Q

I

A

Z

X

A

U

F

D

E

A

V

Z

K

B

H

F

C

Z

U

M

P

F

E

I

J

A

F

R

Z

L

E

I

Z

D

A

U

B

C

H

A

X

S

K

X

U

E

L

X

P

Y

M

H

F

I

N

U

D

Q

D

V

L

W

I

P

I

N

E

P

O

F

O

P

K

I

F

P

I

C

K

E

X

T

G

B

Q

C

S

K

J

N

G

Y

E

G

N

I

J

T

G

N

J

B

N

I

P

M

W

O

E

K

P

Y

N

M

F

N

A

M

R

P

A

H

K

E

W

G

I

O

X

Z

X

I

G

E

C

L

W

Y

E

N

K

F

U

O

X

O

X

G

I

G

K

J

G

P

Q

P

J

O

R

B

I

K

V

Z

W

C

Q

N

Y

P

I

T

K

Y

P

N

J

N

M

A

D

T

H

Z

E

K

M

O

P

D

S

U

Q

E

H

U

W

D

N

S

M

I

B

M

X

T

C

L

W

O

E

T

W

X

I

E

V

C

Z

F

B

S

W

N

T

P

N

L

H

I

G

D

K

M

B

X

A

J

A

J

A

H

N

Q

S

M

R

G

I

A

S

U

C

K

E

L

E

U

R

E

H

R

Y

B

M

R

A

R

K

Y

N

E

J

I

X

P

T

P

E

Y

V

S

T

D

M

T

N

S

P

I

N

Q

Z

S

P

C

X

Q

T

L

I

U

N

W

S

X

C

O

B

L

G

R

L

B

F

O

H

P

I

L

U

D

B

K

N

J

H

C

V

J

C

P

G

A

I

X

Y

J

Q

G

R

Y

Q

C

S

T

G

D

S

N

Y

T

C

O

R

K

U

R

V

E

K

D

W

A

G

D

P

Y

H

I

Q

I

P

T

G

C

U

L

R

X

V

A

B

D

W

N

S

M

U

I

T

F

J

H

R

I

U

L

T

R

U

L

G

O

N

H

T

C

K

P

H

V

C

N

H

S

L

V

M

Q

Z

W

P

O

I

H

E

C

H

V

C

N

G

S

F

E

J

B

E

U

C

J

F

P

O

X

V

P

N

L

H

C

Y

N

T

L

K

D

S

P

A

H

N

K

B

Q

H

C

F

U

I

T

K

H

G

X

J

S

Q

S

H

W

T

D

W

S

H

Q

J

N

D

T

J

R

N

L

M

G

U

R

H

D

M

O

B

M

I

E

B

R

L

V

H

N

X

A

P

J

S

L

H

B

K

U

E

H

J

E

H

D

S

E

D

G

D

S

E

P

K

E

A

E

M

E

C

P

E

O

K

O

U

X

H

V

I

Z

I

N

Y

B

Q

I

M

Y

Z

Y

W

K

S

B

E

G

L

E

I

C

H

S

C

H

E

N

K

L

I

G

X

B

M

I

A

R

P

L

X

K

O

J

Q

T

X

M

V

A

S

J

E

B

R

S

U

S

W

I

S

A

J

F

A

S

W

S

N

M

U

J

Q

T

C

P

J

Y

I

V

T

C

E

N

D

N

O

A

C

X

N

A

U

X

U

E

S

E

F

E

T

Y

R

C

R

D

U

W

Z

X

J

A

F

W

M

E

C

W

L

C

H

W

T

X

M

F

W

S

K

U

W

T

I

R

G

H

B

S

W

B

P

C

T

A

T

S

U

N

I

T

L

W

L

A

Z

L

P

J

U

I

B

K

I

B

U

G

V

E

K

N

W

O

B

H

Z

O

V

O

H

T

H

A

T

A

R

L

I

X

G

P

O

Q

R

I

N

S

G

N

R

I

F

U

T

R

K

D

Q

V

I

M

F

B

X

W

Z

A

U

Q

Y

A

W

T

E

M

N

R

O

Z

N

K

W

K

S

K

L

G

S

E

G

Q

T

Y

N

F

T

Y

F

S

B

S

T

M

Q

D

O

M

R

W

F

W

K

Y

N

E

Y

R

P

G

E

I

U

D

F

N

E

I

R

I

O

X

W

Q

G

V

P

I

N

K

L

N

Q

E

T

J

K

H

R

E

C

H

T

W

I

N

K

L

I

G

E

C

S

W

H

L

X

P

Z

K

G

L

V

C

V

N

B

J

V

C

U

B

D

A

U

W

L

G

O

Y

A

N

K

D

G

T

U

F

T

C

I

E

X

A

V

I

O

T

O

L

F

B

Q

D

K

X

L

D

R

O

Y

N

K

C

I

N

A

X

C

L

E

N

Z

Y

H

N

M

B

N

V

Z

R

F

B

Q

I

S

B

U

Z

S

Y

S

G

Q

Z

W

P

F

W

I

R

P

G

M

K

L

N

B

M

L

U

K

B

I

L

J

T

C

M

P

D

B

P

A

U

R

F

N

Y

T

Q

C

O

P

R

W

K

F

Y

Q

K

L

H

G

A

B

R

Q

E

H

Y

J

T

P

Z

C

D

U

B

I

D

I

O

L

P

U

W

K

F

A

F

Z

H

C

I

M

R

S

C

B

G

B

E

G

T

R

L

S

K

V

C

F

D

Q

V

M

V

T

K

M

H

C

A

P

J

B

P

R

M

K

X

Z

T

G

M

L

Y

H

M

U

F

X

G

N

F

R

P

X

B

D

X

M

E

Z

E

J

E

O

H

M

A

N

A

J

I

Y

L

Z

M

D

S

V

U

A

R

O

T

Y

D

J

C

T

G

K

T

R

E

L

W

A

J

L

C

U

L

I

U

K

O

L

Q

T

O

Q

S

T

W

K

Q

P

O

E

G

H

N

M

B

H

I

B

Z

S

G

U

J

Z

I

F

A

T

A

N

Q

O

I

S

M

T

S

Z

V

Z

B

H

E

C

Z

L

E

Q

D

V

D

V

W

P

F

B

Z

D

L

A

Z

N

S

F

S

L

D

N

G

A

V

J

W

S

A

R

S

K

E

W

G

C

B

P

W

A

X

H

V

G

D

L

Q

U

M

G

D

E

R

K

S

J

H

L

Q

C

N

H

W

S

Q

X

V

J

B

I

N

C

X

U

W

T

M

J

N

L

A

B

O

V

W

B

W

B

L

T

P

V

U

Y

A

Z

S

M

Y

H

K

Q

N

A

S

R

A

U

E

O

T

L

T

X

J

N

C

L

M

H

P

U

W

H

G

I

X

V

P

N

T

X

R

U

Q

T

R

Z

R

Z

T

P

K

C

P

B

P

K

Z

K

S

J

A

S

M

B

C

E

F

P

G

X

C

V

Q

Z

L

V

X

V

G

B

T

E

I

H

T

O

M

L

W

G

Y

___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________
___________________

Ich bin der Thales-Clown

Eigentlich, müsstest du jetzt doch alles verstanden haben, oder?

Die nachstehenden Aufgaben kannst du in Absprache mit deinem Lehrer oder deiner Lehrerin bearbeiten!

Kategorie: -leicht-

Aufgabe

1. Arbeitsauftrag:

Bearbeite dieses Arbeitsblatt:Arbeitsblatt:Kategorie leicht
Hier gibts die Lösungen dazu:Lösungen zu Arbeitsblatt:Kategorie leicht

Kategorie: -mittelschwierig-

Aufgabe

2. Arbeitsauftrag:

Bearbeite dieses Arbeitsblatt:Arbeitsblatt:Kategorie mittelschwierig
Hier gibts die Lösungen dazu:Lösungen zu Arbeitsblatt:Kategorie mittelschwierig

Kategorie: -schwierig-

Aufgabe

3. Arbeitsauftrag:

Bearbeite dieses Arbeitsblatt:Arbeitsblatt:Kategorie schwierig
Hier gibts die Lösungen dazu:Lösungen zu Arbeitsblatt:Kategorie schwierig

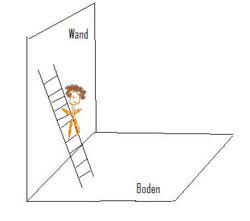
Die folgende Aufgabe ist zum Knüffeln für Profis gedacht!!!

Die rutschende Leiter:

Ziehe an dem grünen Punkt B

Anmerkungen und Arbeitsauftrag

Was fällt dir auf, wenn du am grünen Punkt B ziehst?

Der Satz des Thales findet Anwendung beim Lösen dieses Problems.

Aufgabe

Viel Spaß beim Tüfteln:

Stelle dir vor, eine Leiter (hier die Strecke AB) lehnt an einer Wand.
Die Person, die auf der Leiter steht, befindet sich exakt in der Mitte der Strecke AB.
Frage: Hast du eine Idee auf welchem geometrischen Ort sich die Person befindet, wenn die Leiter von der Wand abrutscht?
Hier hast du einen Lösungsvoschlag:Die rutschende Leiter

Weitere Informationen erhaltet ihr auch auf dieser Homepage:
Die rutschende Leiter - Universität Bayreuth

Entstanden unter Mitwirkung von:

Nico Stahl

@@ Zeile 145: / Zeile 145: @@
 [[Bild:ThalesClownPro_NicoStahl.jpg|thumb|center|500px|Ich bin der Thales-Clown]]
 <br>
-: '''Jetzt versuchen wir das Ganze ein bisschen abtrakter anzugehen, ok?'''
+: '''Jetzt versuchen wir das Ganze ein bisschen abstrakter anzugehen, ok?'''
 <br>
 : '''Orientiere dich einfach bei der kommenden Aufgabe an die Fragestellungen bei Station II und Station III.'''
@@ Zeile 359: / Zeile 359: @@
 : '''Waagrecht und senkrecht, gefundene Wörter werden grün markiert.'''
 <br>
+: '''Die Lösungen können senkrecht, waagrecht und diagonal verlaufen.'''
+<br>
 ===Siebte Station:===
 <br>

Übungsaufgaben zum Satz des Thales: Unterschied zwischen den Versionen

Version vom 9. Juli 2009, 08:27 Uhr