Satz des Pythagoras: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
| − | <br>Das war leicht, oder?<br> | + | <br><br>Das war leicht, oder?<br> |
| + | Die Fläche dieser Quadrate (A) kann man sogar ausrechnen.<br> | ||
| + | Weißt du noch wie das geht? Schauen wir uns doch dazu ein Quadrat einmal genauer an: | ||
| + | <br> | ||
| + | [[Bild:Florianheimerl_Viereck_a.png]] | ||
| + | <br> | ||
| + | {{versteckt|Die Fläche des Quadrats (A) berechnet man mit der Formel Länge mal Breite.}} | ||
| + | <quiz display="simple"> | ||
| + | {Wie rechnet man die Fläche eines Quadrats aus?} | ||
| + | - A = a+a+a+a | ||
| + | + A = aˑa = a² | ||
| + | - A = a:b:c | ||
| + | </quiz> | ||
<br> | <br> | ||
== Der Satz des Pythagoras == | == Der Satz des Pythagoras == | ||
Version vom 15. September 2010, 13:49 Uhr
 Lernpfad
|
Der Satz des Pythagoras funktioniert bei allen Dreiecken mit einem rechten Winkel.
Du bist ja nun schon ein richtiger Dreieck-Experte.
Wie war das noch gleich mit dem rechtwinkligen Dreieck?
 |
In einem rechtwinkligen Dreieck heißt die längste Seite immer Hypotenuse und die anderen beiden Seiten Katheten. |
In dieser Zeichnung habe ich dir ein rechtwinkliges Dreieck mitgebracht.
Ich habe über jeder Kathete und über der Hypotenuse jeweils ein Quadrat gemalt.
Die Seiten des Quadrats sind immer genauso lang wie die jeweilige Kathete oder Hypotenuse.
Wenn du auf „Abspielen“ drückst, kannst du dir anschauen, wie ich es gezeichnet habe.
Das war leicht, oder?
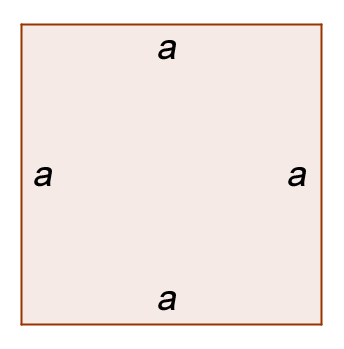
Die Fläche dieser Quadrate (A) kann man sogar ausrechnen.
Weißt du noch wie das geht? Schauen wir uns doch dazu ein Quadrat einmal genauer an:
Der Satz des Pythagoras
Sind a,b,c die Seiten eines rechtwinkligen Dreiecks mit c als Hypotenuse, so gilt :
a² + b² = c²
In Worten : Die Summe der Quadrate über den Katheten ist gleich dem Quadrat über der Hypotenuse.
Umkehrung: Gilt in einem Dreieck a²+b²=c², dann ist dieses Dreieck rechtwinklig und der rechte Winkel liegt gegenüber von c.
