Modellieren im Mathematikunterricht: Unterschied zwischen den Versionen
| Zeile 29: | Zeile 29: | ||
<br>Als Ergebnis erhalte ich 570m³. <br> Leider kann man sich Kubikmeter nur schlecht vorstellen und außerdem trinkt man keine Kubikmeter trinkt, sondern Liter. Deshalb scheint die Umrechnung von m³ in Liter hilfreich. | <br>Als Ergebnis erhalte ich 570m³. <br> Leider kann man sich Kubikmeter nur schlecht vorstellen und außerdem trinkt man keine Kubikmeter trinkt, sondern Liter. Deshalb scheint die Umrechnung von m³ in Liter hilfreich. | ||
<br>Beides sind Volumeneinheiten: | <br>Beides sind Volumeneinheiten: | ||
| − | <br>1m³ <math>\widehat{=}</math>1 00dm³ | + | <br>1m³ <math>\widehat{=}</math>1 00dm³ <math>\Rightarrow</math> 570m³ <math>\widehat{=}</math> 570 000 dm³. |
<br>1dm³ <math>\widehat{=}</math> 1 Liter. | <br>1dm³ <math>\widehat{=}</math> 1 Liter. | ||
| − | <br>570 000 dm³ <math>\widehat{=}</math> 570 000 Liter. | + | <br><math>\Rightarrow</math> 570 000 dm³ <math>\widehat{=}</math> 570 000 Liter. |
In das Schwimmbecken passen also 570 000 Liter Wasser. | In das Schwimmbecken passen also 570 000 Liter Wasser. | ||
Version vom 24. September 2010, 15:00 Uhr
Beispielaufgabe
Wie lange würde es dauern ein Schwimmbecken auzutrinken?
Ich lese mir die Aufgabe also als erstes durch. Da ich schon öfters in einem Schwimmbad war, weiß ich, wie ein Schwimmbecken aussieht.
Ich erstelle also eine Skizze:
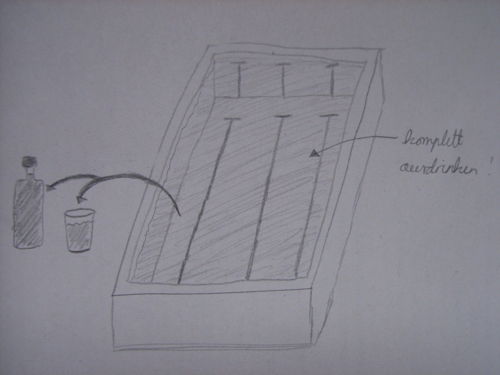
Da das Becken ja ausgetrunken werden soll, muss ich mir zuerst Gedanken darüber machen, wie viel Wasser sich eigentlich in so einem Schwimmbecken befindet. Dazu muss ich also das Volumen des Beckens berechnen.
Aber wie stelle ich das an?
Nun überlege ich also, welchen Körper ich kenne, der einem Schwimmbecken ähnelt. Außerdem weiß ich, dass Schwimmbecken in der Regel rechteckig sind. Also lässt sich ein Schwimmbecken wohl gut durch einen Quader beschreiben. (Der Quader stellt hier mein Modell dar!)
Nun weiß ich, dass ich das Volumen eines Quaders berechnen muss, um wissen, wie viel Wasser sich in einem Schwimmbecken befindet.
Ich mache mir also noch mal eine Skizze:
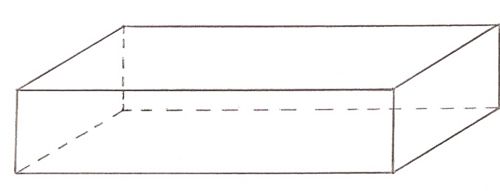
Wie geht noch mal gleich die Volumenformel für einen Quader? Ein Blick in die Formelsammlung verrät: V = a
bc, wobei a, b und c offensichtlich für die Länge, Breite und Tiefe bzw. Höhe des Beckens stehen.
Gut, aber wie lang sind denn die einzelnen Größen?
Da keine weiteren Angaben über die Größe des Beckens gemacht wurden, muss ich mir selber Gedanken machen und die Größen evt. schätzen. Durch meine Schwimmbadbesuche weiß ich, dass es sowohl Becken gibt, die 25 Meter lang sind, als auch welche, die 50 Meter lang sind. Ich entscheide mich hier mal für ein 25 Meter-Becken.
Was ist mit der Tiefe?
In manchen Schwimmbädern ist das Becken auf der einen Seite tiefer, als auf der anderen. Um es nicht unnötig kompliziert zu machen, gehen wir hier aber von einer einheitlichen Größe aus.
Nehmen wir also an, dass das gesamte Becken 1,90 Meter tief ist.
Für die Breite hilft mir die Überlegung, wie viele Bahnen das Schwimmbecken wohl hat. Für diese Aufgabe gehe ich mal von 6 Bahnen aus. Eine einzelne Bahn wird wohl etwa 2 Meter breit sein. Also, ist das gesamte Becken 12 Meter breit.
Nun hab ich alle benötigten Daten zusammen und kann sie in meine Skizze eintragen.
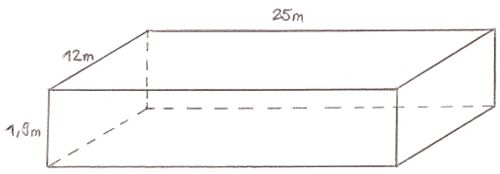
Der nächste Schritt ist nicht schwer. Ich muss die gesammelten Daten in meine Formel einsetzen und ausrechnen: V = 25m1,9m12m = 570m³
Als Ergebnis erhalte ich 570m³.
Leider kann man sich Kubikmeter nur schlecht vorstellen und außerdem trinkt man keine Kubikmeter trinkt, sondern Liter. Deshalb scheint die Umrechnung von m³ in Liter hilfreich.
Beides sind Volumeneinheiten:
1m³ 
1 00dm³ 
570m³ 570 000 dm³.
1dm³ 1 Liter.
570 000 dm³ 570 000 Liter.
In das Schwimmbecken passen also 570 000 Liter Wasser.
Gut, aber wie lang würde ich nun brauchen, um es auszutrinken? Dazu überlege ich, wie viel Liter ein Mensch im Laufe des Tages trinkt. Für einen gesunden Menschen werden 1,5 Liter Flüssigkeit am Tag empfohlen. In einem Jahr wären das dann 1,5*365=547,5 Liter. Für die 570 000 Liter des Schwimmbeckens bräuchte man dann also 570 000/547,5=1041,09589 Jahre. Naja, da ich keine 1041 Jahre leben werde, kann ich es also in meinem Leben nicht schaffen.
Aber wie viele Leute bräuchte ich denn, damit es an einem Tag gelingt? Dazu teile ich das Volumen des Beckens durch die 1,5 Liter, die jeder Mensch am Tag trinken sollte: 570 000 / 1,5 = 380 000. Man bräuchte also 380 000 Menschen, um das Becken im Laufe eines Tages leer zu trinken.
Nur mal zum Vergleich: Würzburg hat 133 195 Einwohner. Man bräuchte also gut 2,5-mal so viele Einwohner, um das Becken leer zu trinken.
Hier geht's zur Seite der Gruppe Gauß
Hier geht's zur Seite der Gruppe Pythagoras
